
| A. | g($\frac{1}{5}$)>g($\frac{8}{5}$)>0 | B. | g($\frac{1}{5}$)$>0>g(\frac{8}{5})$ | C. | g($\frac{8}{5}$)>g($\frac{1}{5}$)>0 | D. | g($\frac{1}{5}$)=g($\frac{8}{5}$)>0 |
分析 利用三角函数的恒等变换求得f(x)的解析式,利用函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,再利用诱导公式、正弦函数的单调性,可得g($\frac{1}{5}$) 和g($\frac{8π}{5}$) 大小关系.
解答 解:把函数f(x)=cos2($\frac{π}{2}$x-$\frac{π}{6}$)=$\frac{1+cos(πx-\frac{π}{3})}{2}$ 的图象向左平移$\frac{1}{3}$个单位后,
得到的函数为g(x)=$\frac{1+cos[π(x+\frac{1}{3})-\frac{π}{3}]}{2}$=$\frac{1+cosπx}{2}$的图象,
故有g($\frac{1}{5}$)=$\frac{1}{2}$+$\frac{1}{2}$cos$\frac{π}{5}$=$\frac{1}{2}$+cos($\frac{π}{2}$-$\frac{3π}{10}$)=$\frac{1}{2}$+sin$\frac{3π}{10}$,g($\frac{8}{5}$)=$\frac{1}{2}$+cos$\frac{8π}{5}$=$\frac{1}{2}$-cos$\frac{3π}{5}$=$\frac{1}{2}$-cos($\frac{π}{2}$+$\frac{π}{10}$)=$\frac{1}{2}$+sin$\frac{π}{10}$,
而sin$\frac{3π}{10}$>sin$\frac{π}{10}$>0,∴g($\frac{1}{5}$)>g($\frac{8π}{5}$)>0,
故选:A.
点评 本题主要考查三角函数的恒等变换、函数y=Asin(ωx+φ)的图象变换规律、诱导公式、正弦函数的单调性的应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| 看营养说明 | 不看营养说明 | 合计 | |
| 男大学生 | 26 | 6 | 32 |
| 女大学生 | 14 | 18 | 32 |
| 合计 | 40 | 24 | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
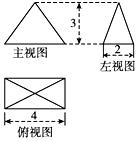
| A. | 8 | B. | 8+4$\sqrt{10}$ | C. | 4$\sqrt{10}$+2$\sqrt{13}$ | D. | 2$\sqrt{10}$+$\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
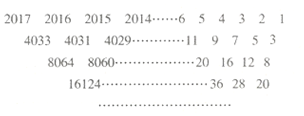 “杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,辑录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( )
“杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,辑录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( )| A. | 2017×22016 | B. | 2018×22015 | C. | 2017×22015 | D. | 2018×22016 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com