
| A. | 53 | B. | 56 | C. | 55 | D. | 57 |
分析 根据题意,由乘法原理可得a、b的取法都有8种,即logab的可能情况有8×8=64种,由对数的性质分析其中重复的情况,在全部数目中将重复的排除即可得答案.
解答 解:根据题意,a、b∈{2,3,4,5,6,7,8,9},
则a、b的取法都有8种,即logab的可能情况有8×8=64种,
其中当a=b时,logab=1,有8种情况是重复的,
log24=log39=2,有2种情况是重复的,
log32=log94,有2种情况是重复的,
log42=log93=$\frac{1}{2}$,有2种情况是重复的,
log23=log49,有2种情况是重复的,
则logab的不同取值有64-7-1-1-1-1=53种;
故选:A.
点评 本题考查排列组合的应用,涉及对数的运算,注意其中对数值相等,即取值重复的情况.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
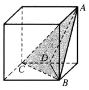 如图是一个正方体,A,B,C为三个顶点,D是棱的中点,则三棱锥A-BCD的正视图,俯视图是(注:选项中的上图是正视图,下图是俯视图)( )
如图是一个正方体,A,B,C为三个顶点,D是棱的中点,则三棱锥A-BCD的正视图,俯视图是(注:选项中的上图是正视图,下图是俯视图)( )| A. | 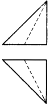 | B. | 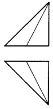 | C. | 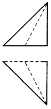 | D. | 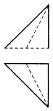 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | g($\frac{1}{5}$)>g($\frac{8}{5}$)>0 | B. | g($\frac{1}{5}$)$>0>g(\frac{8}{5})$ | C. | g($\frac{8}{5}$)>g($\frac{1}{5}$)>0 | D. | g($\frac{1}{5}$)=g($\frac{8}{5}$)>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (?p)∧q | B. | p∧q | C. | p∧(?q) | D. | p∨(?q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
| 频数 | 20 | 40 | 20 | 10 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{n+1}{n+2}$ | B. | $\frac{n+1}{2n+4}$ | C. | $\frac{3}{2}$-$\frac{2n+3}{(n+1)(n+2)}$ | D. | $\frac{3}{4}$-$\frac{2n+3}{2(n+1)(n+2)}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2
如图,在四棱锥P-ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com