Question

10．如图，在四棱锥P-ABCD中，AB⊥平面BCP，CD∥平面ABP，AB=BC=CP=BP=2CD=2
（1）证明：平面ABP⊥平面ADP；
（2）若直线PA与平面PCD所成角为α，求sinα的值．

Answer 1

分析 （1）取AP的中点E，PB的中点F，连结DE，EF，CF，利用平行四边形得出DE∥CF，通过证明CF⊥平面APB得出DE⊥平面PAB，于是平面ABP⊥平面ADP；
（2）将几何体补成直三棱柱，作出线面角，从而可求出sinα的值．

解答 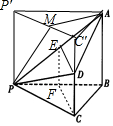（1）证明：取AP的中点E，PB的中点F，连结DE，EF，CF，
则EF$\stackrel{∥}{=}$$\frac{1}{2}$AB，
∵CD∥平面ABP，CD?平面ABCD，平面ABCD∩平面ABP=AB，
∴CD∥AB，又CD=$\frac{1}{2}$AB，
∴EF$\stackrel{∥}{=}$CD，
∴四边形DEFC是平行四边形，∴CF∥DE，
∵AB⊥平面BCP，CF?平面BCP，
∴AB⊥CF，
∵BC=CP=BP，
∴CF⊥PB，又PB∩AB=B，
∴CF⊥平面ABP，
∴DE⊥平面ABP，又DE?平面ADP，
∴平面ABP⊥平面ADP．
（2）解：过P作PP′∥AB，使得PP′=2，延长CD到C′，使得CC′=2，连结AC′，AP′，C′P′，
则直三棱柱PBC-P′AC′所有棱长均为2，
取P′C′的中点M，连结AM，则AM⊥平面PCC′P′，
∴∠APM是直线AP与平面PCD所成的角，即∠APM=α，
∵AM=$\sqrt{AP{′}^{2}-P′{M}^{2}}$=$\sqrt{3}$，PA=$\sqrt{P{B}^{2}+A{B}^{2}}$=2$\sqrt{2}$，
∴sinα=sin∠APM=$\frac{AM}{AP}$=$\frac{\sqrt{3}}{2\sqrt{2}}$=$\frac{\sqrt{6}}{4}$．

点评 本题考查了面面垂直的判定，直线与平面所成角的计算，属于中档题．