
| 分组(单位:岁) | 频数 | 频率 |
| [20,25) | 5 | 0.050 |
| [25,30) | ① | 0.200 |
| [30,35) | 35 | ② |
| [35,40) | 30 | 0.300 |
| [40,45) | 10 | 0.100 |
| 合计 | 100 | 1.00 |
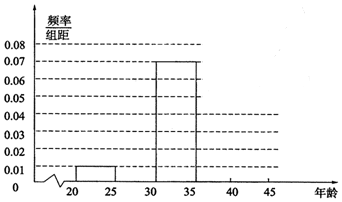
分析 (Ⅰ)利用已知条件真假在①处填20,②处填0.350;补全频率分布直方图.求出500名职工中年龄在[30,35)的人数.
(Ⅱ)用分层抽样的方法,从中选取20人,则其中“年龄低于30岁”的有5人,“年龄不低于30岁“的有15人.故X的可能取值为0,1,2;求出概率,得到分布列,然后求解期望即可.
解答 解:(Ⅰ)①处填20,②处填0.350;…(2分)
补全频率分布直方图如图所示: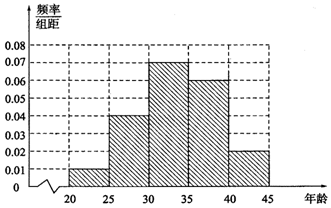
…(4分)
500名职工中年龄在[30,35)的人数为0.35×500=175人,…(6分)
(Ⅱ)用分层抽样的方法,从中选取20人,则其中“年龄低于30岁”的有5人,“年龄不低于30岁“的有15人.故X的可能取值为0,1,2;$P(X=0)=\frac{{C_{15}^2}}{{C_{20}^2}}=\frac{42}{76}=\frac{21}{38}$.$P(X=1)=\frac{{C_{15}^1C_5^1}}{{C_{20}^2}}=\frac{30}{76}=\frac{15}{38}$.$P(X=2)=\frac{C_5^2}{{C_{20}^2}}=\frac{4}{76}=\frac{1}{19}$…(9分)
所以X的分布列为
| X | 0 | 1 | 2 |
| P | $\frac{21}{38}$ | $\frac{15}{38}$ | $\frac{1}{19}$ |
点评 本题考查分层抽样,离散型随机变量的分布列以及期望的求法,频率分布直方图的应用,考查计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
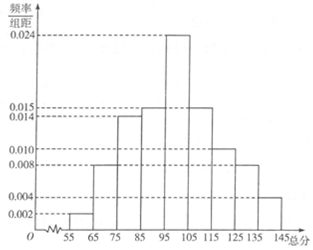 某省组织了一次高考模拟考试,该省教育部门抽取了1000名考生的数学考试成绩,并绘制成频率分布直方图如图所示.
某省组织了一次高考模拟考试,该省教育部门抽取了1000名考生的数学考试成绩,并绘制成频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2016 | B. | -2017 | C. | 2016 | D. | 2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com