
分析 (Ⅰ)由已知及正弦定理可得2sinAsinC=sinCcosA,由于sinC≠0,可求tanA=$\frac{1}{3}$,且A为锐角,利用同角三角函数基本关系式可求sinA的值.
(Ⅱ)利用同角三角函数基本关系式可求可得cosA,利用两角和的正弦函数公式可求sinC,由正弦定理可得c=2$\sqrt{2}$a,进而利用三角形面积公式即可计算得解.
解答 (本题满分为14分)
(Ⅰ)∵3asinC=ccosA.
∴2sinAsinC=sinCcosA,…2分
∵sinC≠0,
∴tanA=$\frac{1}{3}$,且A为锐角,…4分
∴sinA=$\frac{\sqrt{10}}{10}$…7分
(Ⅱ)由(Ⅰ)可得cosA=$\sqrt{1-si{n}^{2}A}$=$\frac{3\sqrt{10}}{10}$,
∴sinC=sin(A+B)=sin(A+$\frac{π}{4}$)=$\frac{2\sqrt{5}}{5}$,
由正弦定理可得$\frac{a}{c}=\frac{sinA}{sinC}$=$\frac{\sqrt{2}}{4}$,c=2$\sqrt{2}$a,
∵S=$\frac{1}{2}$acsinB=$\frac{1}{2}a×2\sqrt{2}a×\frac{\sqrt{2}}{2}$=a2=9,
∴a=3.
点评 本题主要考查了正弦定理,同角三角函数基本关系式,两角和的正弦函数公式,三角形面积公式在解三角形中的应用,考查了计算能力和转化思想,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
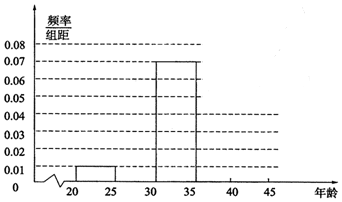
| 分组(单位:岁) | 频数 | 频率 |
| [20,25) | 5 | 0.050 |
| [25,30) | ① | 0.200 |
| [30,35) | 35 | ② |
| [35,40) | 30 | 0.300 |
| [40,45) | 10 | 0.100 |
| 合计 | 100 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=3,n=3,输入的a依次为由小到大顺序排列的质数(从最小质数开始),
中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=3,n=3,输入的a依次为由小到大顺序排列的质数(从最小质数开始),| A. | 9 | B. | 27 | C. | 32 | D. | 103 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [5,+∞) | B. | (5,+∞) | C. | (-∞,5] | D. | (-∞,5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com