
分析 (1),在回归直线y=0.5x-85中,y的值是一个估算值;
(2),由P(X2>6.635)≈0.01,可判断有99%的把握认为两个事件有关;
(3),由-2≤|x+1|-|x-1|≤2,则k的取值范围是k<2
(4),正态分布曲线关于直线x=0对称,则P(ξ<-1.96)=(1-0.95)×$\frac{1}{2}$
解答 解:对于(1),在回归直线y=0.5x-85中,变量x=200时,变量y的值大约是15,这是一个估算值,故错误.
对于(2),根据2×2列联表中的数据计算得出X2=7.469,而P(X2>6.635)≈0.01,则有99%的把握认为两个事件有关,故正确;
对于(3),∵-2≤|x+1|-|x-1|≤2,∴若不等式|x+1|-|x-1|>k有解,则k的取值范围是k<2,故错;
对于(4),机变量ζ满足正态分布N(0,1),则正态分布曲线关于直线x=0对称,若P(|ξ|≤1.96)=0.950,则P(ξ<-1.96)=(1-0.95)×$\frac{1}{2}$.故错.
故答案为:(2)
点评 题考查了回归直线的性质、独立性检验的基本思想,绝对值不等式、正态分布,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,e2) | D. | (e2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 664 | B. | 844 | C. | 968 | D. | 1204 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | -1 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±2x | B. | y=±$\frac{2\sqrt{5}}{5}$ | C. | y=±$\frac{\sqrt{5}}{2}$x | D. | y=±$\frac{1}{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
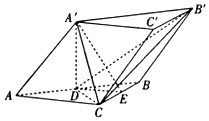 在斜三棱柱ABC-A′B′C′中,AC=BC=A′A=A′C,A′在底面ABC上的射影为AB的中点D,E为线段BC的中点.
在斜三棱柱ABC-A′B′C′中,AC=BC=A′A=A′C,A′在底面ABC上的射影为AB的中点D,E为线段BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com