
分析 (1)将曲线C1消去参数,即可求得曲线的普通方程,求得曲线C2的直角坐标方程,联立即可求得M点坐标;
(2)求得曲线C3的直角坐标方程,利用点的坐标公式,圆心到直线的距离,即可求得|AB|的最小值.
解答 解:(1)曲线C1的参数方程为$\left\{\begin{array}{l}{x=cosα}\\{y=si{n}^{2}α}\end{array}\right.$(α为参数),消去参数α,
整理得:y+x2=1,x∈[-1,1],①
曲线C2:ρcos(θ-$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$,则x+y+1=0,②
联立①②,消去y可得:x2-x-2=0,x=-1,x=2(舍去),
∴M(-1,0);
(2)曲线C3:ρ=2sinθ,则x2+(y-1)2=1,则以(0,1)为圆心,半径r=1,
设圆心C,点C,B到直线x+y+1=0的距离分别为d,d′
则d=$\frac{丨0+1+1丨}{\sqrt{2}}$=$\sqrt{2}$,
丨AB丨≥d′≥d-r=$\sqrt{2}$-1,
∴丨AB丨的最小值为$\sqrt{2}$-1
点评 本题考查抛物线的参数方程,圆的极坐标方程,直线圆的位置关系,考查计算能力,属于基础题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:解答题
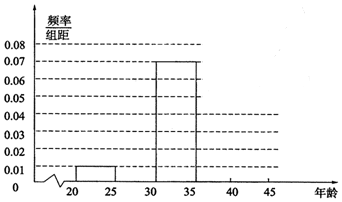
| 分组(单位:岁) | 频数 | 频率 |
| [20,25) | 5 | 0.050 |
| [25,30) | ① | 0.200 |
| [30,35) | 35 | ② |
| [35,40) | 30 | 0.300 |
| [40,45) | 10 | 0.100 |
| 合计 | 100 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 套餐费(元) | 免费主叫时长(分钟) | 免费主叫时长收费(元/分钟) | 免费数据流量(MB) | 超出数据流量收费(元/MB) |
| 38 | 50 | 0.25 | 300 | 0.29 |
| 48 | 50 | 0.25 | 500 | 0.29 |
| 58 | 100 | 0.19 | 500 | 0.29 |
| 88 | 220 | 0.19 | 700 | 0.29 |
| A. | 60分钟和300 MB | B. | 70分钟和500 MB | C. | 100分钟和650 MB | D. | 150分钟和550 MB |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [5,+∞) | B. | (5,+∞) | C. | (-∞,5] | D. | (-∞,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 39 | B. | 21 | C. | 39或21 | D. | 21或36 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=±\frac{1}{4}x$ | B. | $y=±\frac{1}{3}x$ | C. | $y=±\frac{1}{2}x$ | D. | y=±x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com