
分析 (1)求出函数f(x)的定义域与 f′(x),通过当a<0时,当a>0时,判断导函数的符号,推出单调性与极值.
(2)化简g(x),求出g′(x),利用g(x)在区间(a,3)上有最值,说明g(x)在区间(a,3)上有极值,方程g'(x)=0在(a,3)上有一个或两个不等实根,列出不等式组,转化为对任意a∈[1,2],g′(a)=3a2+(m+2a)a-1=5a2+ma-1<0恒成立,得到m<$\frac{1-5{a}^{2}}{a}$=$\frac{1}{a}-5a$,然后求解即可.
解答 解:(1)由已知得f(x)的定义域为(0,+∞),且 f′(x)=$\frac{1}{x}$-a,…(2分)
当a<0时,$f'(x)=\frac{1}{x}-a>0$,
∴f(x)在(0,+∞)单调增,f(x)无极值;…(3分)
当a>0时,
由$f'(x)=\frac{1}{x}-a>0得:0<x<\frac{1}{a}$,由$f'(x)=\frac{1}{x}-a<0得:x>\frac{1}{a}$,
∴$f(x)在(0,\frac{1}{a})上单调递增,在(\frac{1}{a},+∞)上单调递减$.…(4分)
∴$f(x)的极大值f(\frac{1}{a})=-(lna+4)$,无极小值. …(5分)
综上:当a<0时,f(x)无极值;
当a>0时,$f(x)有极大值f(\frac{1}{a})=-(lna+4)$,无极小值. …(6分)
(2)g(x)=x3+$\frac{{x}^{2}}{2}$[m-2f′(x)]=x3+($\frac{m}{2}$+a)x2-x,
∴g′(x)=3x2+(m+2a)x-1,
∵g(x)在区间(a,3)上有最值,
∴g(x)在区间(a,3)上有极值,即方程g'(x)=0在(a,3)上有一个或两个不等实根,
又g′(0)=-1,∴$\left\{\begin{array}{l}{g′(a)<0}\\{g′(3)>0}\end{array}\right.$,…(9分)
由题意知:对任意a∈[1,2],g′(a)=3a2+(m+2a)a-1=5a2+ma-1<0恒成立,
∴m<$\frac{1-5{a}^{2}}{a}$=$\frac{1}{a}-5a$,因为a∈[1,2],∴m<$-\frac{19}{2}$
对任意a∈[1,2],g′(3)=26+3m+6a>0恒成立
∴m>$\frac{-6a-26}{3}$=$-\frac{26}{3}-2a$,
∵a∈[1,2],∴m>-$\frac{32}{3}$,
∴-$\frac{32}{3}<m<-\frac{19}{2}$.…(12分)
点评 本题考查函数的导数的综合应用,函数恒成立,考查分类讨论思想以及转化思想的应用,考查计算能力.


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 重合 | B. | 形状相同,位置不同 | ||
| C. | 关于y轴对称 | D. | 形状不同,位置不同 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:(1)SG⊥平面EFG;(2)SD⊥平面EFG;(3)GF⊥平面SEF;(4)EF⊥平面GSD;(5)GD⊥平面SEF.正确的是( )
如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:(1)SG⊥平面EFG;(2)SD⊥平面EFG;(3)GF⊥平面SEF;(4)EF⊥平面GSD;(5)GD⊥平面SEF.正确的是( )| A. | (1)和(3) | B. | (2)和(5) | C. | (1)和(4) | D. | (2)和(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2+2$\sqrt{2}$ | B. | 2$\sqrt{2}$-2 | C. | $\sqrt{5}$+2 | D. | $\sqrt{5}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
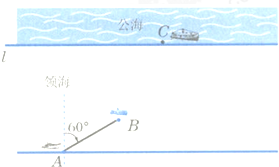 设直线l为公海的分界线,一巡逻艇在A处发现了北偏东60°的海面B处有一艘走私船,走私船正向停泊在公海上接应的走私海轮C航行,以便上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,A与公海相距约为20海里,走私船可能向任一方向逃窜,请回答下列问题:
设直线l为公海的分界线,一巡逻艇在A处发现了北偏东60°的海面B处有一艘走私船,走私船正向停泊在公海上接应的走私海轮C航行,以便上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,A与公海相距约为20海里,走私船可能向任一方向逃窜,请回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
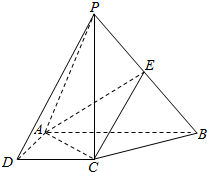 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,BC=$\sqrt{2}$,且PC⊥CD,BC⊥PA,E是PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,BC=$\sqrt{2}$,且PC⊥CD,BC⊥PA,E是PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com