Question

如图，在三棱柱ABC-A₁B₁C₁中，已知AB⊥侧面BB₁C₁C，AB=BC=1，BB₁=2，∠BCC₁=60°．
（Ⅰ）求证：C₁B⊥平面ABC；
（Ⅱ）设

CE

=λ

CC1

（0≤A≤1），且平面AB₁E与BB₁E所成的锐二面角的大小为30°，试求λ的值．

Answer 1

考点：用空间向量求平面间的夹角,直线与平面垂直的判定,二面角的平面角及求法

专题：空间位置关系与距离,空间角

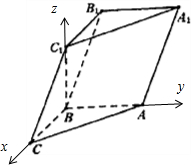
分析：（Ⅰ）证明AB⊥BC₁，在△CBC₁中，由余弦定理求解BC1=

3

，然后证明BC⊥BC₁，利用直线与平面垂直的判定定理证明C₁B⊥平面ABC．
（Ⅱ）通过AB，BC，BC₁两两垂直．以B为原点，BC，BA，BC₁所在直线为x，y，z轴建立空间直角坐标系．求出相关点的坐标，求出平面AB₁E的一个法向量，平面的一个法向量通过向量的数量积，推出λ的方程，求解即可．

解答： 解：（Ⅰ）证明：因为AB⊥平面BB₁C₁C，BC₁⊆平面BB₁C₁C，所以AB⊥BC₁，…（1分）
在△CBC₁中，BC=1，CC₁=BB₁=2，∠BCC₁=60°，
由余弦定理得：BC12=BC2+CC12-2BC•CC1•cos∠BCC1=1²+2²-2×1×2×cos60°=3，
所以BC1=

3

，…（3分）
故BC2+BC12=CC12，所以BC⊥BC₁，…（5分）
又BC∩AB=B，∴C₁B⊥平面ABC．…（6分）
（Ⅱ）由（Ⅰ）可知，AB，BC，BC₁两两垂直．以B为原点，BC，BA，BC₁所在直线
为x，y，z轴建立空间直角坐标系．

则B(0，0，0)，  A(0，1，0)，  C(1，0，0)，  C1(0，0，

3

)，B1(-1，0，

3

)．…（7分）
所以

CC1

=(-1，0，

3

)，所以

CE

=(-λ，0，

3

λ)，∴E(1-λ，0，

3

λ)，
则

AE

=(1-λ，-1，

3

λ)，

AB1

=(-1，-1，

3

)．…（8分）
设平面AB₁E的一个法向量为

n

=(x，y，z)，
则

n ⊥ AE n ⊥ AB1

，得

(1-λ)x-y+ 3 λz=0 -x-y+ 3 z=0

，
令z=

3

，则x=

3-3λ

2-λ

，  y=

3

2-λ

，∴

n

=(

3-3λ

2-λ

，

3

2-λ

，

3

)，…（9分）
．∵AB⊥平面BB₁C₁C，

BA

=(0，1，0)是平面的一个法向量，…（10分）
∴|cos＜

n

，

BA

＞|=

| n • BA |

| n |•| BA |

=

3 2-λ

1× ( 3-3λ 2-λ )2+( 3 2-λ )2+( 3 )2

=

3

2

．
两边平方并化简得2λ²-5λ+3=0，所以λ=1或λ=

3

2

（舍去）．
∴λ=1…（12分）

点评：本题考查直线与平面垂直的判定定理的应用，二面角的向量求解方法，考查空间想象能力计算能力以及逻辑推理能力．