
分析 (Ⅰ)求出|FM|,|OM|,利用△OFM(O为原点)的面积为$\frac{{\sqrt{2}}}{4}$及过点A(1,1),建立方程组,即可求双曲线的方程;
(Ⅱ)设BC的方程为y-1=k(x-1)+m,双曲线方程可化为2[(x-1)+1]2-[(y-1)+1]2=1,利用k1,k2是关于K的方程(m+2)K2-(4+2k)K+4k-2m=0的两个根,即可证明结论.
解答 (Ⅰ)解:双曲线渐近线方程为bx±ay=0,
焦点可设为F(c,0),其中$c=\sqrt{{a^2}+{b^2}}$,则$|{FM}|=\frac{{|{bc±a•0}|}}{{\sqrt{{b^2}+{a^2}}}}=\frac{bc}{c}=b,|{OM}|=\sqrt{{c^2}-{b^2}}=a$,
故△OFM的面积为$\frac{ab}{2}$.…(3分)
由条件可知求得$\left\{\begin{array}{l}\frac{1}{a^2}-\frac{1}{b^2}=1\\ \frac{ab}{2}=\frac{{\sqrt{2}}}{4}\end{array}\right.$求得${a^2}=\frac{1}{2},{b^2}=1$,
故双曲线的方程为2x2-y2=1.…(5分)
(Ⅱ)证明:设BC的方程为y-1=k(x-1)+m,
双曲线方程可化为2[(x-1)+1]2-[(y-1)+1]2=1,
即2(x-1)2-(y-1)2+4(x-1)-2(y-1)=0,
因此2m(x-1)2-m(y-1)2+4(x-1)[(y-1)-k(x-1)]-2(y-1)[(y-1)-k(x-1)]=0,
(2m-4k)(x-1)2-(m+2)(y-1)2+(4+2k)(x-1)(y-1)=0,$({m+2}){({\frac{y-1}{x-1}})^2}-({4+2k})•\frac{y-1}{x-1}+4k-2m=0$.
因此k1,k2是关于K的方程(m+2)K2-(4+2k)K+4k-2m=0的两个根.…(9分)
${k_1}+{k_2}=\frac{4+2k}{m+2},{k_1}•{k_2}=\frac{4k-2m}{m+2}$.
由条件可知$-2={k_1}+{k_2}+{k_1}{k_2}=\frac{4+2k}{m+2}+\frac{4k-2m}{m+2}=\frac{6k+4-2m}{m+2}?k=-\frac{4}{3}$,
故直线BC的斜率为定值$-\frac{3}{4}$.…(12分)
点评 本题考查双曲线的方程与性质,考查直线与双曲线位置关系的运用,考查韦达定理,属于中档题.


科目:高中数学 来源: 题型:解答题
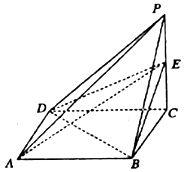 如图,已知四棱锥P-ABCD是边长为1的正方形,PB=PD=$\sqrt{5}$,PC=2,E是侧棱PC上的动点.
如图,已知四棱锥P-ABCD是边长为1的正方形,PB=PD=$\sqrt{5}$,PC=2,E是侧棱PC上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②③ | B. | ①④ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com