
分析 使用正弦定理用sinA,sinC表示出a,c,得出a+c关于A的三角函数,根据A的范围和正弦函数的性质得出a+c的最值.
解答 解:由正弦定理得$\frac{a}{sinA}=\frac{c}{sinC}=\frac{b}{sinB}=\frac{1}{sin60°}$=$\frac{2\sqrt{3}}{3}$.
∴a=$\frac{2\sqrt{3}}{3}sinA$,c=$\frac{2\sqrt{3}}{3}sinC$=$\frac{2\sqrt{3}}{3}sin(\frac{2π}{3}-A)$.
∴a+c=$\frac{2\sqrt{3}}{3}$sinA+$\frac{2\sqrt{3}}{3}sin(\frac{2π}{3}-A)$=$\frac{2\sqrt{3}}{3}$($\frac{3}{2}sinA$+$\frac{\sqrt{3}}{2}cosA$)=2sin(A+$\frac{π}{6}$).
∵0<A<$\frac{2π}{3}$,∴$\frac{π}{6}$<A+$\frac{π}{6}$<$\frac{5π}{6}$.
∴$\frac{1}{2}<$sin(A+$\frac{π}{6}$)≤1.∴1<2sin(A+$\frac{π}{6}$)≤2.
∴a+c的取值范围是(1,2].
点评 本题考查了正弦定理得应用,两角和差的三角函数,正弦函数的图象与性质,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | a、b、c 成等差数列 | B. | a、b、c成等比数列 | ||
| C. | a、2b、3c 成等差数列 | D. | a、2b、3c成等比数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | -4 | C. | -6 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
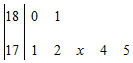 (文科)某校女子篮球队7名运动员身高(单位:厘米)分布的茎叶图如图,已知记录的平均身高为175cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末尾数记为x,那么x的值为2.
(文科)某校女子篮球队7名运动员身高(单位:厘米)分布的茎叶图如图,已知记录的平均身高为175cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末尾数记为x,那么x的值为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com