
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 的最小值;
的最小值;
(2)若![]() ,且
,且![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(1)当![]() 时,
时,![]() ,先求导可得
,先求导可得![]() ,设
,设![]() ,利用导函数可判断
,利用导函数可判断![]() 在
在![]() 上单调递增,由
上单调递增,由![]() ,即可判断
,即可判断![]() 的单调性,进而求解;
的单调性,进而求解;
(2)先求导可得![]() ,容易得到
,容易得到![]() 在
在![]() 上单调递增,由
上单调递增,由![]() ,即可判断
,即可判断![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,设
上单调递增,设![]() ,则
,则![]() ,
,![]() ,设
,设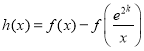 ,利用导函数可判断
,利用导函数可判断![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ,即
,即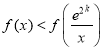 ,则可得
,则可得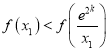 ,即
,即 ,进而由
,进而由![]() 的单调性求证即可.
的单调性求证即可.
(1)解:当![]() 时,
时,![]() ,
,
所以![]() ,
,
设![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
即![]() 在
在![]() 上单调递增,
上单调递增,
因为![]() ,
,
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
因此![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() .
.
(2)证明:![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递增,因为
上单调递增,因为![]() ,
,
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
因此,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
由![]() ,不妨设
,不妨设![]() ,则
,则![]() ,
,![]() ,
,
令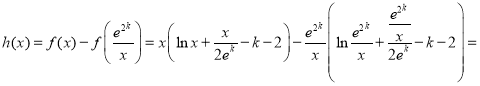
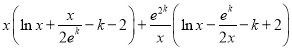 ,
,
则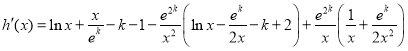
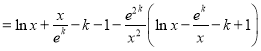
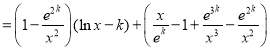
![]() ,
,
当![]() 时,
时,![]() ,
,
故![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
所以当![]() 时,
时,![]() 即
即![]() 时,
时,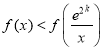 ,
,
因此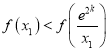 ,
,
又![]() ,所以
,所以 ,
,
因为![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() ,故
,故![]() .
.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:高中数学 来源: 题型:
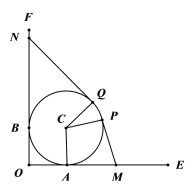
【题目】某地开发一片荒地,如图,荒地的边界是以C为圆心,半径为1千米的圆周.已有两条互相垂直的道路OE,OF,分别与荒地的边界有且仅有一个接触点A,B.现规划修建一条新路(由线段MP,![]() ,线段QN三段组成),其中点M,N分别在OE,OF上,且使得MP,QN所在直线分别与荒地的边界有且仅有一个接触点P,Q,
,线段QN三段组成),其中点M,N分别在OE,OF上,且使得MP,QN所在直线分别与荒地的边界有且仅有一个接触点P,Q,![]() 所对的圆心角为
所对的圆心角为![]() .记∠PCA=
.记∠PCA=![]() (道路宽度均忽略不计).
(道路宽度均忽略不计).
(1)若![]() ,求QN的长度;
,求QN的长度;
(2)求新路总长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为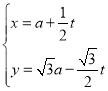 (t为参数,
(t为参数,![]() ).在以坐标原点为极点、x轴的非负半轴为极轴的极坐标系中,曲线C的极坐标方程为
).在以坐标原点为极点、x轴的非负半轴为极轴的极坐标系中,曲线C的极坐标方程为![]() .
.
(1)若点![]() 在直线l上,求线l的直角坐标方程和曲线C的直角坐标方程;
在直线l上,求线l的直角坐标方程和曲线C的直角坐标方程;
(2)已知![]() ,点P在直线l上,点Q在曲线C上,且
,点P在直线l上,点Q在曲线C上,且![]() 的最小值为
的最小值为![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点S( -2,0) ,T(2,0),动点P为平面上一个动点,且直线SP、TP的斜率之积为![]() .
.
(1)求动点P的轨迹E的方程;
(2)设点B为轨迹E与y轴正半轴的交点,是否存在直线l,使得l交轨迹E于M,N两点,且F(1,0)恰是△BMN的垂心?若存在,求l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数集![]() ,其中
,其中![]() ,且
,且![]() ,若对
,若对![]() ,
,![]() 与
与![]() 两数中至少有一个属于
两数中至少有一个属于![]() ,则称数集
,则称数集![]() 具有性质
具有性质![]() .
.
(1)分别判断数集![]() 与数集
与数集![]() 是否具有性质
是否具有性质![]() ,说明理由;
,说明理由;
(2)已知数集![]() 具有性质
具有性质![]() ,判断数列
,判断数列![]() ,
,![]() ,…,
,…,![]() 是否为等差数列,若是等差数列,请证明;若不是,请说明理由.
是否为等差数列,若是等差数列,请证明;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点F2是双曲线![]() 的右焦点,动点A在双曲线左支上,直线l1:tx﹣y+t﹣2=0与直线l2:x+ty+2t﹣1=0的交点为B,则|AB|+|AF2|的最小值为( )
的右焦点,动点A在双曲线左支上,直线l1:tx﹣y+t﹣2=0与直线l2:x+ty+2t﹣1=0的交点为B,则|AB|+|AF2|的最小值为( )
A.8B.![]() C.9D.
C.9D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
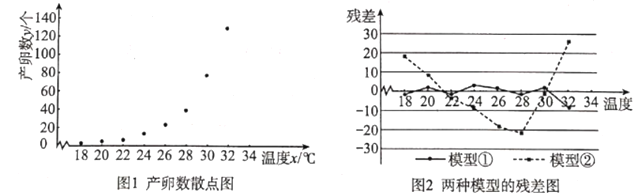
【题目】红铃虫(Pectinophora gossypiella)是棉花的主要害虫之一,其产卵数与温度有关.现收集到一只红铃虫的产卵数y(个)和温度x(℃)的8组观测数据,制成图1所示的散点图.现用两种模型①![]() ,②
,②![]() 分别进行拟合,由此得到相应的回归方程并进行残差分析,进一步得到图2所示的残差图.
分别进行拟合,由此得到相应的回归方程并进行残差分析,进一步得到图2所示的残差图.
根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
|
25 | 2.89 | 646 | 168 | 422688 | 48.48 | 70308 |
表中![]() ;
;![]() ;
;![]() ;
;![]() ;
;
(1)根据残差图,比较模型①、②的拟合效果,应选择哪个模型?并说明理由;
(2)根据(1)中所选择的模型,求出y关于x的回归方程(系数精确到0.01),并求温度为34℃时,产卵数y的预报值.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为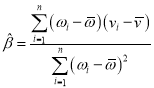 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国制造2025》是经国务院总理李克强签批,由国务院于2015年5月印发的部署全面推进实施制造强国的战略文件,是中国实施制造强国战略第一个十年的行动纲领.制造业是国民经济的主体,是立国之本、兴国之器、强国之基.发展制造业的基本方针为质量为先,坚持把质量作为建设制造强国的生命线.某制造企业根据长期检测结果,发现生产的产品质量与生产标准的质量差都服从正态分布N(μ,σ2),并把质量差在(μ﹣σ,μ+σ)内的产品为优等品,质量差在(μ+σ,μ+2σ)内的产品为一等品,其余范围内的产品作为废品处理.优等品与一等品统称为正品.现分别从该企业生产的正品中随机抽取1000件,测得产品质量差的样本数据统计如下:
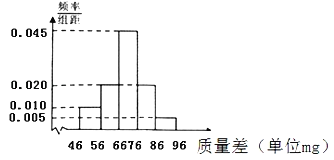
(1)根据频率分布直方图,求样本平均数![]()
(2)根据大量的产品检测数据,检查样本数据的方差的近似值为100,用样本平均数![]() 作为μ的近似值,用样本标准差s作为σ的估计值,求该厂生产的产品为正品的概率.(同一组中的数据用该组区间的中点值代表)
作为μ的近似值,用样本标准差s作为σ的估计值,求该厂生产的产品为正品的概率.(同一组中的数据用该组区间的中点值代表)
[参考数据:若随机变量ξ服从正态分布N(μ,σ2),则:P(μ﹣σ<ξ≤μ+σ)≈0.6827,P(μ﹣2σ<ξ≤μ+2σ)≈0.9545,P(μ﹣3σ<ξ≤μ+3σ)≈0.9973.
(3)假如企业包装时要求把3件优等品球和5件一等品装在同一个箱子中,质检员每次从箱子中摸出三件产品进行检验,记摸出三件产品中优等品球的件数为X,求X的分布列以及期望值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com