
 如图,两个椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1,$\frac{{y}^{2}}{25}$+$\frac{{x}^{2}}{9}$=1内部重叠区域的边界记为曲线C,P是曲线C上任意一点,给出下列三个判断:
如图,两个椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1,$\frac{{y}^{2}}{25}$+$\frac{{x}^{2}}{9}$=1内部重叠区域的边界记为曲线C,P是曲线C上任意一点,给出下列三个判断:| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 ①,若点P在椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1上,P到F1(-4,0)、F2(4,0)两点的距离之和为定值、到E1(0,-4)、E2(0,4)两点的距离之和不为定值;
②,两个椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1,$\frac{{y}^{2}}{25}$+$\frac{{x}^{2}}{9}$=1关于直线y=x、y=-x均对称,曲线C关于直线y=x、y=-x均对称;
③,曲线C所围区域在边长为6的正方形内部.
解答 解:对于①,若点P在椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1上,P到F1(-4,0)、F2(4,0)两点的距离之和为定值、到E1(0,-4)、E2(0,4)两点的距离之和不为定值,故错;
对于②,两个椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1,$\frac{{y}^{2}}{25}$+$\frac{{x}^{2}}{9}$=1关于直线y=x、y=-x均对称,曲线C关于直线y=x、y=-x均对称,故正确;
对于③,曲线C所围区域在边长为6的正方形内部,所以面积必小于36,故正确.
故选:C
点评 本题考查了椭圆的定义及对称性,属于基础题.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 将6辆不同的小汽车和2辆不同的卡车驶入如图所示的10个车位中的某8个内,其中2辆卡车必须停在A与B的位置,那么不同的停车位置安排共有40320种?(结果用数值表示)
将6辆不同的小汽车和2辆不同的卡车驶入如图所示的10个车位中的某8个内,其中2辆卡车必须停在A与B的位置,那么不同的停车位置安排共有40320种?(结果用数值表示)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{16}{9},2})$ | B. | $({\frac{16}{9},+∞})∪({-∞,0})$ | C. | $({\frac{16}{9},2}]$ | D. | $({\frac{2}{3},2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{2}}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
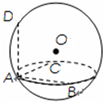 如图,设A、B、C、D为球O上四点,若AB、AC、AD两两互相垂直,且AB=AC=$\sqrt{6}$,AD=2,则球O的体积为$\frac{32π}{3}$.
如图,设A、B、C、D为球O上四点,若AB、AC、AD两两互相垂直,且AB=AC=$\sqrt{6}$,AD=2,则球O的体积为$\frac{32π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-1)>f($\frac{\sqrt{3}}{3}$) | B. | f($\sqrt{2}$)>f(-$\sqrt{2}$) | C. | f(4)>f(3) | D. | f(-$\sqrt{2}$)>f($\sqrt{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com