
分析 (1)把x=ρcosθ,y=ρsinθ代入曲线C的极坐标方程化直角坐标方程,利用x+y=x+$\frac{1}{4}{x}^{2}$=$\frac{1}{4}(x+2)^{2}$-1,即可得出结论;
(2)将直线的参数方程代入曲线C的直角坐标方程,利用根与系数的关系结合t的几何意义求得|AB|的最小值.
解答 解:(1)由ρcos2θ=4sinθ,得(ρcosθ)2=4ρsinθ,
把x=ρcosθ,y=ρsinθ代入上式,得x2=4y,
∴曲线C的直角坐标方程为x2=4y,
∵M(x,y)为曲线C上的任意一点,
∴x+y=x+$\frac{1}{4}{x}^{2}$=$\frac{1}{4}(x+2)^{2}$-1≥-1,
∴x+y的取值范围是[-1,+∞);
(2)将直线l的参数方程代入x2=4y,得t2cos2α-4tsinα-4=0,
设A、B两点对应的参数分别为t1,t2,
则|AB|=|t1-t2|=$\frac{4}{co{s}^{2}α}$,当cos2α=1时,|AB|的最小值为4.
点评 本题考查极坐标方程化直角坐标方程,考查直线参数方程中参数几何意义的应用,是基础题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
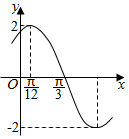 函数$f(x)=Asin({ωx+ϕ})({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,
函数$f(x)=Asin({ωx+ϕ})({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $-\frac{2}{3}$ | C. | $\frac{{\sqrt{5}}}{3}$ | D. | $-\frac{{\sqrt{5}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .an=3n-1 | B. | an=2n+1 | C. | .an=2n+3 | D. | .an=3n+2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com