
分析 (1)圆的方程x2+y2-2x-2my+2m2-4m+1=0化为(x-1)2+(y-m)2=-m2+4m,当-m2+4m>0时表示圆,半径最大时,-m2+4m取得最大值,求出对应m的值;
(2)圆周上到直线l的距离等于1的点有且只有3个时,圆心到直线l的距离d=r-1,列出方程求出k的值.
解答 解:(1)圆的方程x2+y2-2x-2my+2m2-4m+1=0可化为:
(x-1)2+(y-m)2=-m2+4m,
它表示圆时,应有-m2+4m>0,
解得0<m<4;
当半径最大时,应有-m2+4m最大,
此时m=2,圆的方程为 x2+y2-2x-4y+1=0;
(2)圆的方程x2+y2-2x-4y+1=0,化为(x-1)2+(y-2)2=4;
该圆的圆周上到直线l:2kx-2y+4+$\sqrt{3}$-3k=0的距离等于1的点有且只有3个,
则圆心(1,2)到直线l的距离d等于半径r-1,
即$\frac{|2k-2×2+4+\sqrt{3}-3k|}{\sqrt{{4k}^{2}+4}}$=1,
化简得${(k-\sqrt{3})}^{2}$=4k2+4,
解得k=-$\frac{\sqrt{3}}{3}$.
点评 本题主要考查直线和圆的方程与应用问题,点到直线的距离公式的应用,也体现了转化的数学思想,是综合性题目.


科目:高中数学 来源: 题型:解答题
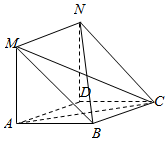 如图,在菱形ABCD中,MA⊥平面ABCD,且四边形ADNM是平行四边形.已知MA=3,AD=4,∠BAD=60°.
如图,在菱形ABCD中,MA⊥平面ABCD,且四边形ADNM是平行四边形.已知MA=3,AD=4,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题①,②均为真命题 | B. | 命题②,③均为假命题 | ||
| C. | 命题②,④均为假命题 | D. | 命题①,③,④均为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com