
分析 根据平方差函数的定义分别进行验证判断即可.
解答 解:(1)若f(x)=$\left\{\begin{array}{l}{1,x≥0}\\{0,x<0}\end{array}\right.$,
则当x=2,y=1时,
则f2(x)-f2(y)=f2(2)-f2(1)=1-1=0,
f(x+y)f(x-y)=f(3)f(1)=1×1=1,
则f2(x)-f2(y)≠f(x+y)f(x-y),
则f(x)不是“平方差函数”;故(1)错误,
(2)若f(x)=kx(k>0),
则f2(x)-f2(y)=k2x2-k2y2=k2(x2-y2),
f(x+y)f(x-y)=k(x+y)•k(x-y)=k2(x2-y2),
满足f2(x)-f2(y)=f(x+y)f(x-y),f(x)为“平方差函数”;故(2)正确,
(3)若f2(x)-f2(y)=f(x+y)f(x-y),
则令x=y=0,则f2(0)-f2(0)=f(0)f(0)=0,
则f(0)=0,
令x=0,则f2(0)-f2(y)=f(y)f(-y),
即-f2(y)=f(y)f(-y),
∵f(x)是定义在R上的不恒为零的函数,
∴-f(y)=f(-y),
即函数f(-x)=-f(x),则f(x)是奇函数,
则若f(x)为“平方差函数”,则f(x)为奇函数正确,故(3)正确;
(4)若f(x)=-x,则f2(x)-f2(y)=x2-y2,f(x+y)f(x-y)=-(x+y)•[-(x-y)]=x2-y2,
满足f2(x)-f2(y)=f(x+y)f(x-y),即f(x)为“平方差函数”,则f(x)此时为减函数,故(4)错误.
故答案为:(2)(3)
点评 本题主要考查命题的真假判断,涉及函数的奇偶性和单调性的性质,正确理解平方差函数的定义是解决本题的关键.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
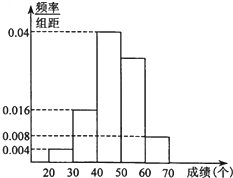 体育课上,李老师对初三(1)班50名学生进行跳绳测试.现测得他们的成绩(单位:个)全部介于20到70之间,将这些成绩数据进行分组(第一组:(20,30],第二组:(30,40],…,第五组:(60,70]),并绘制成如图所示的频率分布直方图.
体育课上,李老师对初三(1)班50名学生进行跳绳测试.现测得他们的成绩(单位:个)全部介于20到70之间,将这些成绩数据进行分组(第一组:(20,30],第二组:(30,40],…,第五组:(60,70]),并绘制成如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com