
分析 (1)直接利用基本不等式求解即可;
(2)y=$\frac{{x}^{2}}{{x}^{4}+9}$=$\frac{1}{{x}^{2}+\frac{9}{{x}^{2}}}$,再利用基本不等式求解.
解答 解:(1)∵0<x<$\frac{5}{3}$,
∴3x>0,5-3x>0.
由基本不等式可得y=3x(5-3x)≤$[\frac{3x+(5-3x)}{2}]^{2}$=$\frac{25}{4}$,
当且仅当3x=5-3x,即x=$\frac{5}{6}$时,函数有最大值$\frac{25}{4}$;
(2)∵x≠0,∴y=$\frac{{x}^{2}}{{x}^{4}+9}$=$\frac{1}{{x}^{2}+\frac{9}{{x}^{2}}}$≤$\frac{1}{6}$,
当且仅当x2=$\frac{9}{{x}^{2}}$,即x=$±\sqrt{3}$时,函数有最大值$\frac{1}{6}$.
点评 本题考查基本不等式的运用,考查学生的计算能力,要注意基本不等式的使用条件.


科目:高中数学 来源: 题型:选择题
| A. | 120 | B. | 240 | C. | 360 | D. | 480 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
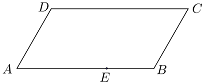 图为一块平行四边形园地ABCD,经测量,AB=20米,BC=10米,∠ABC=120°,拟过线段AB上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将该园地分为面积之比为3:1的左、右两部分分别种植不同的花卉,设EB=x,EF=y(单位:米)
图为一块平行四边形园地ABCD,经测量,AB=20米,BC=10米,∠ABC=120°,拟过线段AB上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将该园地分为面积之比为3:1的左、右两部分分别种植不同的花卉,设EB=x,EF=y(单位:米)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最小值8 | B. | 有最大值8 | C. | 有最小值4$\sqrt{5}$ | D. | 有最大值4$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{3}{2}$,2] | B. | [$\frac{\sqrt{5}}{2}$,2] | C. | [$\frac{3}{2}$,$\sqrt{5}$] | D. | [$\frac{\sqrt{5}}{2}$,$\sqrt{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |$\overrightarrow{a}$-$\overrightarrow{b}$|=1 | B. | ($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{b}$ | C. | ($\overrightarrow{a}$-$\overrightarrow{b}$)•($\overrightarrow{a}$+$\overrightarrow{b}$)=$\frac{5}{2}$ | D. | ($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{b}$=-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com