
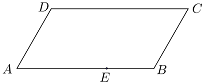
 ͼΪһ��ƽ���ı�����ABCD����������AB=20�ף�BC=10�ף���ABC=120�㣬����߶�AB��һ��E���һ��ֱ·EF����F���ı���ABCD�ı��ϣ�����·�Ŀ��ȣ��������ط�Ϊ���֮��Ϊ3��1�����������ֱַ���ֲ��ͬ�Ļ��ܣ���EB=x��EF=y����λ���ף�
ͼΪһ��ƽ���ı�����ABCD����������AB=20�ף�BC=10�ף���ABC=120�㣬����߶�AB��һ��E���һ��ֱ·EF����F���ı���ABCD�ı��ϣ�����·�Ŀ��ȣ��������ط�Ϊ���֮��Ϊ3��1�����������ֱַ���ֲ��ͬ�Ļ��ܣ���EB=x��EF=y����λ���ף����� ��1������F���C�غ�ʱ��S��BEC=$\frac{1}{4}$S?ABCD����$\frac{1}{2}$•EB•h=$\frac{1}{4}$AB•h���Ӷ�ȷ����E��λ�ã�
��2����E���߶�AB�ϣ���10��x��20��0��x��10������ȷ��y����x�ĺ�����ϵʽ���Ӷ����÷ֶκ�����ã���0��x��10ʱ��y=2$\sqrt{{x}^{2}-5x+25}$���ɶ��κ�������Сֵ����10��x��20ʱ��y=$\sqrt{{x}^{2}+\frac{10000}{{x}^{2}}+100}$���ɻ�������ʽ����ֵ���Ӷ��ɵã�
��� �⣺��1������F���C�غ�ʱ��S��BEC=$\frac{1}{4}$S?ABCD����$\frac{1}{2}$•EB•h=$\frac{1}{4}$AB•h��
����hΪƽ���ı���AB���ϵĸߣ���EB=$\frac{1}{2}$AB������E��AB���е㣮
��2���ߵ�E���߶�AB�ϣ�
��0��x��20��
��10��x��20ʱ���ɣ�1��֪����F���߶�BC�ϣ�
��AB=20m��BC=10m����ABC=120�㣬
��S?ABCD=AB•BC•sin��ABC=20��10��$\frac{\sqrt{3}}{2}$=100$\sqrt{3}$��
��S��EBF=$\frac{1}{2}$x•BF•sin120��=25$\sqrt{3}$����BF=$\frac{100}{x}$��
�������Ҷ����ã�
y=EF=$\sqrt{{x}^{2}+��\frac{100}{x}��^{2}-2x•\frac{100}{x}•cos120��}$=$\sqrt{{x}^{2}+\frac{10000}{{x}^{2}}+100}$��
��0��x��10ʱ����F���߶�CD�ϣ�
��S�ı���EBCF=$\frac{1}{2}$��x+CF����10��sin60��=25$\sqrt{3}$��CF=10-x��
��BE��CFʱ��EF=$\sqrt{1{0}^{2}+��2x-10��^{2}-2��10����2x-10��cos120��}$��
��BE��CFʱ��EF=$\sqrt{1{0}^{2}+��10-2x��^{2}-2��10����10-2x��cos60��}$��
�����Ϊy=EF=2$\sqrt{{x}^{2}-5x+25}$��
����������y=$\left\{\begin{array}{l}{2\sqrt{{x}^{2}-5x+25}��0��x��10}\\{\sqrt{{x}^{2}+\frac{10000}{{x}^{2}}+100}��10��x��20}\end{array}\right.$��
��0��x��10ʱ��y=2$\sqrt{{x}^{2}-5x+25}$����x=$\frac{5}{2}$ʱ��y����Сֵymin=5$\sqrt{3}$����ʱCF=$\frac{15}{2}$��
��10��x��20ʱ��y=$\sqrt{{x}^{2}+\frac{10000}{{x}^{2}}+100}$��10$\sqrt{3}$��5$\sqrt{3}$��
�ʵ���E���B2.5m����F���C7.5mʱ��EF��̣��䳤��Ϊ5$\sqrt{3}$��
���� ���⿼���˺�����ʵ�������е�Ӧ�ü���������ʽ����κ���������Ӧ�ã������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
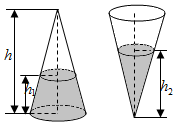 ��ͼ��Բ�������ĸ�Ϊh��Բ��ˮ��ĸ�Ϊh1����$\frac{h_1}{h}$=$\frac{1}{3}$������Բ���ã�ˮ���Ϊh2����$\frac{h_2}{h}$����$\frac{\root{3}{19}}{3}$��
��ͼ��Բ�������ĸ�Ϊh��Բ��ˮ��ĸ�Ϊh1����$\frac{h_1}{h}$=$\frac{1}{3}$������Բ���ã�ˮ���Ϊh2����$\frac{h_2}{h}$����$\frac{\root{3}{19}}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|3��x��7} | B�� | {x|3��x��10} | C�� | {x|3��x��4} | D�� | {x|4��x��7} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����ͦã��¡ͦã�����Φ� | B�� | ��a�Φ£�a��b����b�Φ� | ||
| C�� | ��a�Φ���b�Φ���c��a��c��b����c�ͦ� | D�� | ��a�ͦã�b�ͦã���a��b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2$\sqrt{3}$-1 | B�� | 2$\sqrt{3}$+1 | C�� | 4 | D�� | $\sqrt{6}$+$\sqrt{2}$+1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com