
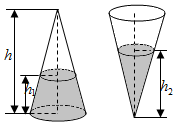
 如图,圆锥形容器的高为h,圆锥内水面的高为h1,且$\frac{h_1}{h}$=$\frac{1}{3}$,若将圆锥倒置,水面高为h2,则$\frac{h_2}{h}$等于$\frac{\root{3}{19}}{3}$.
如图,圆锥形容器的高为h,圆锥内水面的高为h1,且$\frac{h_1}{h}$=$\frac{1}{3}$,若将圆锥倒置,水面高为h2,则$\frac{h_2}{h}$等于$\frac{\root{3}{19}}{3}$. 分析 根据水的体积不变列出方程解出h2.
解答 解:设圆锥形容器的底面积为S,则未倒置前液面的面积为$\frac{4}{9}S$.
∴水的体积V=$\frac{1}{3}$Sh-$\frac{1}{3}$×$\frac{4}{9}S$×(h-h1)=$\frac{19}{81}Sh$.
设倒置后液面面积为S′,则$\frac{S′}{S}$=($\frac{{h}_{2}}{h}$)2,∴S′=$\frac{S{{h}_{2}}^{2}}{{h}^{2}}$.
∴水的体积V=$\frac{1}{3}S′{h}_{2}$=$\frac{S{{h}_{2}}^{3}}{3{h}^{2}}$.
∴$\frac{S{{h}_{2}}^{3}}{3{h}^{2}}$=$\frac{19}{81}Sh$,解得h2=$\frac{\root{3}{19}h}{3}$.
∴$\frac{{h}_{2}}{h}$=$\frac{\root{3}{19}}{3}$.
故答案为:$\frac{\root{3}{19}}{3}$.
点评 本题考查了圆锥的结构特征,圆锥的体积计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{x}$ | B. | y=-x3 | C. | y=${log_{\frac{1}{2}}}$x | D. | y=x+$\frac{1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “x>2”是“x2-2x>0”成立的必要条件 | |
| B. | 已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,则“$\overrightarrow{a}$∥$\overrightarrow{b}$”是“$\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{0}$”的充要条件 | |
| C. | 命题“p:?x∈R,x2≥0”的否定形式为“¬p:?x0∈R,x02≥0” | |
| D. | 命题“若x2=1,则x=1”的逆否命题为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120 | B. | 240 | C. | 360 | D. | 480 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
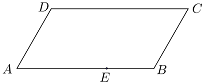 图为一块平行四边形园地ABCD,经测量,AB=20米,BC=10米,∠ABC=120°,拟过线段AB上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将该园地分为面积之比为3:1的左、右两部分分别种植不同的花卉,设EB=x,EF=y(单位:米)
图为一块平行四边形园地ABCD,经测量,AB=20米,BC=10米,∠ABC=120°,拟过线段AB上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将该园地分为面积之比为3:1的左、右两部分分别种植不同的花卉,设EB=x,EF=y(单位:米)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com