
分析 (1)利用条件求得m、n的值,可得函数的解析式,从而求得它的最值.
(2)根据g(x)的解析式,点Q(0,2)在y=g(x)的图象上,求得φ的值,再利用正弦函数的图象的对称性,得出结论.
解答 解:(1)易知f(x)=msin2x-ncos2x,则由它的图象过点$(\frac{π}{12},\sqrt{3})$和点$(\frac{2π}{3},-2)$,
可得$\left\{\begin{array}{l}msin\frac{π}{6}-ncos\frac{π}{6}=\sqrt{3}\\ msin\frac{4π}{3}-ncos\frac{4π}{3}=-2\end{array}\right.$,解得$m=\sqrt{3}\;,\;\;n=-1$.故$f(x)=\sqrt{3}sin2x+cos2x=2sin(2x+\frac{π}{6})$.
故函数f(x)的最大值为2,最小值为-2.
(2)由(1)可知:$g(x)=f(x+φ)=2sin(2x+2φ+\frac{π}{6})$.
于是,当且仅当Q(0,2)在y=g(x)的图象上时满足条件,∴$g(0)=2sin(2ϕ+\frac{π}{6})=2$.由0<ϕ<π,得$φ=\frac{π}{6}$.
故$g(x)=2sin(2x+\frac{π}{2})=2cos2x$.由$2x=kπ+\frac{π}{2}$,得$x=\frac{kπ}{2}+\frac{π}{4}\;\;(k∈Z)$.
于是,函数y=g(x)图象的对称中心为:$(\frac{kπ}{2}+\frac{π}{4},0)(k∈Z)$.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的最值以及它的图象的对称性,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{n(n+1)}$ | B. | $\frac{1}{{2}^{n}}$ | C. | $\frac{3}{(n+1)(n+2)}$ | D. | $\frac{5-2n}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
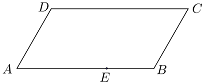 图为一块平行四边形园地ABCD,经测量,AB=20米,BC=10米,∠ABC=120°,拟过线段AB上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将该园地分为面积之比为3:1的左、右两部分分别种植不同的花卉,设EB=x,EF=y(单位:米)
图为一块平行四边形园地ABCD,经测量,AB=20米,BC=10米,∠ABC=120°,拟过线段AB上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将该园地分为面积之比为3:1的左、右两部分分别种植不同的花卉,设EB=x,EF=y(单位:米)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,9] | B. | [9,+∞) | C. | (-∞,9) | D. | (9,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com