
分析 (Ⅰ)根据求导公式和法则求出f′(x),由条件列出方程组求出a、b的值,代入后求出f(x);
(Ⅱ)由(1)求出g(x)并化简,根据求导公式和法则求出g′(x),求出g′(x)=0的根后,由导数与函数单调性的关系求出g(x)的单调区间,由极值的定义求出函数g(x)的极值.
解答 解:(Ⅰ)由题意得,f′(x)=3x2+2ax+b,
∵f'(1)=2a,f'(2)=-b,
∴$\left\{\begin{array}{l}{3+2a+b=2a}\\{12+4a+b=-b}\end{array}\right.$,解得a=$-\frac{3}{2}$,b=-3,
则f(x)=x3$-\frac{3}{2}$x2+3x+1;
(Ⅱ)由(1)得,f′(x)=3x2-3x-3,
∴g(x)=f'(x)e-x=3(x2-x-1)e-x=$3•\frac{{x}^{2}-x-1}{{e}^{x}}$,
∴g′(x)=$3•\frac{{(x}^{2}-x-1)′{e}^{x}-({x}^{2}-x-1)({e}^{x})′}{{(e}^{x})^{2}}$=$3•\frac{-{x}^{2}+3x}{{e}^{x}}$,
由g′(x)=0得x=0或x=3,
∴当0<x<3时,g′(x)>0;当x<0或x>3时g′(x)<0,
∴g(x)在(0,3)上递增,在(-∞,0)和(3,+∞)上递减,
即当x=0时,g(x)取到极小值g(0)=-3,
当x=3时,g(x)取到极大值g(3)=$\frac{15}{{e}^{3}}$.
点评 本题考查了求导公式和法则,导数与函数的单调性、极值的关系,考查了方程思想,化简、变形能力.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:解答题
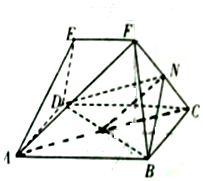 如图,在多面体ABCDEF中,四边形ABCD为矩形,△ADE,△BCF均为等边三角形,EF∥AB,EF=AD=$\frac{1}{2}$AB,N为线段PC的中点.
如图,在多面体ABCDEF中,四边形ABCD为矩形,△ADE,△BCF均为等边三角形,EF∥AB,EF=AD=$\frac{1}{2}$AB,N为线段PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{17}{2}$ | B. | 9 | C. | $\frac{29}{3}$ | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 10 | C. | -8 | D. | -10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
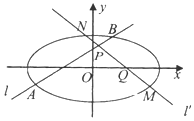 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,过$P({0,\frac{b}{2}})$的直线l与椭圆交于A,B两点,过Q(x0,0)(|x0|<a)的直线l'与椭圆交于M,N两点.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,过$P({0,\frac{b}{2}})$的直线l与椭圆交于A,B两点,过Q(x0,0)(|x0|<a)的直线l'与椭圆交于M,N两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
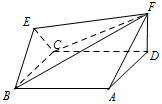 如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且$FD=\sqrt{3}$.
如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且$FD=\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com