
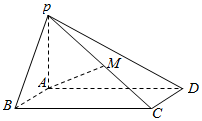
 如图,已知四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,PA=AB=2,AD=4,M为侧棱PC的中点.
如图,已知四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,PA=AB=2,AD=4,M为侧棱PC的中点.分析 (1)以A为原点,建立空间直角坐标系A-xyz,求出$\overrightarrow{AM}$,$\overrightarrow{PB}$的向量坐标,利用向量的数量积直接求解异面直线AM与PB所成角的大小.
(2)求出平面BPC的法向量,AM的向量,利用空间向量的数量积以及直线和平面所成角的定义进行求解即可.
解答  解:(1)如图所示,以A为原点,建立空间直角坐标系A-xyz,
解:(1)如图所示,以A为原点,建立空间直角坐标系A-xyz,
则A(0,0,0),B(2,0,0),D(0,4,0),P(0,0,2),C(2,4,0),M(1,2,1),
∵$\overrightarrow{AM}$=(1,2,1),$\overrightarrow{PB}$=(2,0,-2),
∴$\overrightarrow{AM}$•$\overrightarrow{PB}$=(1,2,1)•(2,0,-2)=1×2-1×2=0,
∴$\overrightarrow{AM}$⊥$\overrightarrow{PB}$,则AM⊥PB,
∴异面直线AM与PD所成角为90°.
(2)设平面BPC的法向量为$\overrightarrow{m}$=(x,y,z),
∵$\overrightarrow{BC}=(0,4,0),\overrightarrow{BP}=(-2,0,2)$,并且$\overrightarrow{m}⊥\overrightarrow{BC},\overrightarrow{m}⊥\overrightarrow{BP}$,
∴$\left\{\begin{array}{l}4y=0\\-2x+2z=0\end{array}\right.$,令x=1得z=1,y=0,
∴平面MBD的一个法向量为$\overrightarrow{m}$=(1,0,1),
∵$\overrightarrow{AM}$=(1,2,1),
∴cos<$\overrightarrow{AM}$,$\overrightarrow{m}$>=$\frac{\overrightarrow{AM}•\overrightarrow{m}}{|\overrightarrow{AM}||\overrightarrow{m}|}$=$\frac{2}{\sqrt{2}•\sqrt{6}}$=$\frac{\sqrt{3}}{3}$,
设直线AM与平面BPC所成角为θ,θ∈(0,$\frac{π}{2}$),
则sinθ=|cos<$\overrightarrow{AM}$,$\overrightarrow{m}$>|=$\frac{\sqrt{3}}{3}$,
∴直线AM与平面BPC所成角的正弦值$\frac{\sqrt{3}}{3}$.
点评 本题考查空间异面直线所成角以及直线和平面所成角的大小的计算,建立坐标系,利用向量法以及向量的数量积是解决本题的关键.考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 在犯错误的概率不超过0.05的前提下,认为打鼾与患心脏病有关 | |
| B. | 约有95%的打鼾者患心脏病 | |
| C. | 在犯错误的概率不超过0.01的前提下,认为打鼾与患心脏病有关 | |
| D. | 约有99%的打鼾者患心脏病 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{h}$=$\frac{1}{R}$+$\frac{1}{r}$ | B. | $\frac{1}{h}$=$\frac{1}{R}$+$\frac{1}{r}$ | C. | $\frac{1}{r}$=$\frac{1}{R}$+$\frac{1}{h}$ | D. | $\frac{2}{R}$=$\frac{1}{r}$+$\frac{1}{h}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
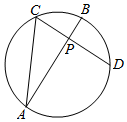 如图,AB、CD是⊙O的两条弦,且AB是线段CD的中垂线,已知AB=6,CD=2$\sqrt{5}$,则线段AC的长度为( )
如图,AB、CD是⊙O的两条弦,且AB是线段CD的中垂线,已知AB=6,CD=2$\sqrt{5}$,则线段AC的长度为( )| A. | 5 | B. | $\sqrt{35}$ | C. | $\sqrt{30}$ | D. | 3$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | ±1 | C. | 2 | D. | ±2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com