
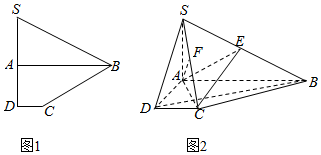
 如图(1)所示,已知四边形SBCD是由直角△SAB和直角梯形ABCD拼接而成的,其中∠SAB=∠SDC=90°,且点A为线段SD的中点,AD=2DC=1,AB=SD,现将△SAB沿AB进行翻折,使得二面角S-AB-C的大小为90°,得到的图形如图(2)所示,连接SC,点E、F分别在线段SB、SC上.
如图(1)所示,已知四边形SBCD是由直角△SAB和直角梯形ABCD拼接而成的,其中∠SAB=∠SDC=90°,且点A为线段SD的中点,AD=2DC=1,AB=SD,现将△SAB沿AB进行翻折,使得二面角S-AB-C的大小为90°,得到的图形如图(2)所示,连接SC,点E、F分别在线段SB、SC上.分析 (Ⅰ)推导出SA⊥AD,SA⊥AB,从而SA⊥平面ABCD,进而SA⊥BD,再求出AC⊥BD,由此得到BD⊥平面SAC,从而能证明BD⊥AF.
(Ⅱ)设点E到平面ABCD的距离为h,由VB-AEC=VE-ABC,且$\frac{{V}_{E-ABC}}{{V}_{S-ABCD}}$=$\frac{2}{5}$,能求出点E到平面ABCD的距离.
解答 证明:(Ⅰ)∵四边形SBCD是由直角△SAB和直角梯形ABCD拼接而成的,其中∠SAB=∠SDC=90°,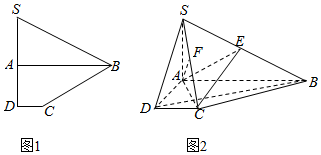
二面角S-AB-C的大小为90°,
∴SA⊥AD,
又SA⊥AB,AB∩AD=A,∴SA⊥平面ABCD,
又BD?平面ABCD,∴SA⊥BD,
在直角梯形ABCD中,∠BAD=∠ADC=90°,
AD=2CD=1,AB=2,
∴tan∠ABD=tan∠CAD=$\frac{1}{2}$,
又∠DAC+∠BAC=90°,
∴∠ABD+∠BAC=90°,即AC⊥BD,
又AC∩SA=A,∴BD⊥平面SAC,
∵AF?平面SAC,∴BD⊥AF.
解:(Ⅱ)设点E到平面ABCD的距离为h,
∵VB-AEC=VE-ABC,且$\frac{{V}_{E-ABC}}{{V}_{S-ABCD}}$=$\frac{2}{5}$,
∴$\frac{{V}_{E-ABC}}{{V}_{S-ABCD}}$=$\frac{\frac{1}{3}{S}_{△ABC}•h}{\frac{1}{3}{S}_{梯形ABCD}•SA}$=$\frac{\frac{1}{2}×2×1×h}{\frac{\frac{5}{2}×1}{2}×1}$=$\frac{2}{5}$,
解得h=$\frac{1}{2}$,
∴点E到平面ABCD的距离为$\frac{1}{2}$.
点评 本题考查线线垂直的证明,考查点到平面的距离的求法,考查等体积法的应用,考查推理论证能力、运算求解能力、空间思维能力,考查转化化归思想、数形结合思想,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{π}{2}+2kπ,π+2kπ}],k∈Z$ | B. | $[{-\frac{π}{2}+3kπ,π+3kπ}],k∈Z$ | ||
| C. | $[{π+2kπ,\frac{5π}{2}+2kπ}],k∈Z$ | D. | $[{π+3kπ,\frac{5π}{2}+3kπ}],k∈Z$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{6}$ | B. | $\frac{\sqrt{6}}{5}$ | C. | $\frac{\sqrt{6}}{4}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
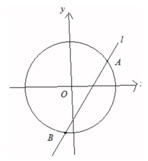 已知椭圆T:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,直线l经过点P(m,0)与T相交于A、B两点.
已知椭圆T:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,直线l经过点P(m,0)与T相交于A、B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{5}{4}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
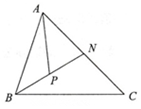
| A. | $\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | B. | -$\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | C. | -$\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ | D. | $\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com