
| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | 4 |
分析 根据题意,将点(2,-1)代入双曲线的方程可得$\frac{1}{{a}^{2}}$-$\frac{4}{4}$=1,解可得a的值,由双曲线的几何性质可得c的值,进而由双曲线离心率公式计算可得答案.
解答 解:根据题意,双曲线$\frac{y^2}{a^2}-\frac{x^2}{4}=1$过点(2,-1),
则有$\frac{1}{{a}^{2}}$-$\frac{4}{4}$=1,
解可得a2=$\frac{1}{2}$,即a=$\frac{\sqrt{2}}{2}$,
b=2,
则c=$\sqrt{\frac{1}{2}+4}$=$\frac{3\sqrt{2}}{2}$,
则双曲线的离心率e=$\frac{c}{a}$=3;
故选:C.
点评 本题考查双曲线的几何性质以及标准方程,关键是求出a的值.


 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,e] | B. | {0,e} | C. | {1,2} | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 根据“2015年国民经济和社会发展统计公报”中公布的数据,从2011 年到2015 年,我国的第三产业在GDP中的比重如下:
根据“2015年国民经济和社会发展统计公报”中公布的数据,从2011 年到2015 年,我国的第三产业在GDP中的比重如下:| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代码x | 1 | 2 | 3 | 4 | 5 |
| 第三产业比重y(%) | 44.3 | 45.5 | 46.9 | 48.1 | 50.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 28 | C. | 12 | D. | 8或28 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
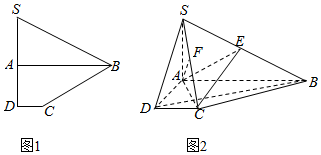 如图(1)所示,已知四边形SBCD是由直角△SAB和直角梯形ABCD拼接而成的,其中∠SAB=∠SDC=90°,且点A为线段SD的中点,AD=2DC=1,AB=SD,现将△SAB沿AB进行翻折,使得二面角S-AB-C的大小为90°,得到的图形如图(2)所示,连接SC,点E、F分别在线段SB、SC上.
如图(1)所示,已知四边形SBCD是由直角△SAB和直角梯形ABCD拼接而成的,其中∠SAB=∠SDC=90°,且点A为线段SD的中点,AD=2DC=1,AB=SD,现将△SAB沿AB进行翻折,使得二面角S-AB-C的大小为90°,得到的图形如图(2)所示,连接SC,点E、F分别在线段SB、SC上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com