
���� ��1������f��x��=$\overrightarrow{m}$•$\overrightarrow{n}$-$\frac{1}{2}$���������������ã����f��x������ʽ��������f��x����ͼ�������������Գ���֮��ľ���Ϊ$\frac{��}{2}$�����أ�������⺯��f��x���ĵ����������䣻
��2������f��B��=0�����B�Ǵ�С������b=$\sqrt{7}$��sinA=3sinC�������Ҷ������a��c�͡�ABC�������
��� �⣺�����⣺$\overrightarrow{m}$=��$\sqrt{3}$sin��x��cos��x����$\overrightarrow{n}$=��cos��x��-cos��x�����أ�0��x��R����
��f��x��=$\overrightarrow{m}$•$\overrightarrow{n}$-$\frac{1}{2}$=$\sqrt{3}$sin��xcos��x-cos2��x$-\frac{1}{2}$=$\frac{\sqrt{3}}{2}$sin2��x$-\frac{1}{2}$cos2��x-1=sin��2��x$-\frac{��}{6}$��-1
���������Գ���֮��ľ���Ϊ$\frac{��}{2}$��
��T=$\frac{2��}{2��}=\frac{��}{2}$��
���=1
����f��x���Ľ���ʽΪ$f��x��=sin��2x-\frac{��}{6}��-1$��
��1����$2k��-\frac{��}{2}��2x-\frac{��}{6}��2k��+\frac{��}{2}����k��-\frac{��}{6}��x��k��+\frac{��}{3}$��
��f��x���ĵ�������Ϊ$[k��-\frac{��}{6}��k��+\frac{��}{3}]��k��Z$��
$\begin{array}{l}��2��f��B��=sin��2B-\frac{��}{6}��-1=0��\\��0��B����\\��-\frac{��}{6}��2B-\frac{��}{6}��\frac{11��}{6}��\\��2B-\frac{��}{6}=\frac{��}{2}��\\��B=\frac{��}{3}��\end{array}$
$\begin{array}{l}sinA=3sinC��\\��a=3c��\end{array}$
�ڡ�ABC�У������Ҷ����ɵã�
$cosB=\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=\frac{{9{c^2}+{c^2}-7}}{{6{c^2}}}=\frac{{10{c^2}-7}}{{6{c^2}}}=\frac{1}{2}$��
��c=1��a=3��
${S_{��ABC}}=\frac{1}{2}acsinB=\frac{1}{2}��3��1��\frac{{\sqrt{3}}}{2}=\frac{{3\sqrt{3}}}{4}$��
���� ���⿼������������������Ǻ����Ļ��������������Ҷ��������ã�������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
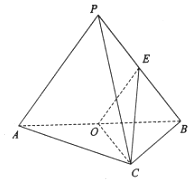 ��֪����P-ABC�У�AC��BC��AC=BC=2��PA=PB=BC=3��O��AB�е㣬E��PB�е㣮
��֪����P-ABC�У�AC��BC��AC=BC=2��PA=PB=BC=3��O��AB�е㣬E��PB�е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �ۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{7{x^2}}}{16}-\frac{y^2}{12}=1$ | B�� | $\frac{y^2}{3}-\frac{x^2}{2}=1$ | C�� | ${x^2}-\frac{y^2}{3}=1$ | D�� | $\frac{{3{y^2}}}{23}-\frac{x^2}{23}=1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
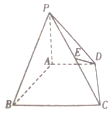 ��ͼ���ڵ���Ϊֱ�����ε�����P-ABCD�У�EΪPC���е㣬AD��BC����ABC=90�㣬PA��ƽ��ABCD��PA=2��AD=2��AB=2$\sqrt{3}$��BC=4��
��ͼ���ڵ���Ϊֱ�����ε�����P-ABCD�У�EΪPC���е㣬AD��BC����ABC=90�㣬PA��ƽ��ABCD��PA=2��AD=2��AB=2$\sqrt{3}$��BC=4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��1�� | B�� | ��0��1] | C�� | ��1��2�� | D�� | ��1��2] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{6}}{6}$ | B�� | $\frac{\sqrt{6}}{5}$ | C�� | $\frac{\sqrt{6}}{4}$ | D�� | $\frac{\sqrt{6}}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com