
分析 (1)根据极值点处的导数为零,结合f(1)=g(-1)-2列出关于a,b的方程组,求出a,b,然后再利用导数研究导数研究单调区间;
(2)①将a=0代入,研究极值的符号,即可求出求b的取值范围,
②结合①的结论,通过适当的变形,利用放缩法和基本不等式即可证明.
解答 解:(1)由已知得f$′(x)=ax+\frac{1}{x}$,(x>0),
所以$f′(\frac{\sqrt{2}}{2})=\frac{\sqrt{2}}{2}a+\sqrt{2}=0$,所以a=-2.
由f′(1)=g(-1)-2,
得a+1=b-2,
所以b=1.
所以h(x)=-x2+lnx+x,(x>0).
则$h′(x)=-2x+\frac{1}{x}+1=\frac{2(x+\frac{1}{2})(x-1)}{-x}$,(x>0),
由h′(x)>0得0<x<1,h′(x)<0得x>1.
所以h(x)的减区间为(1,+∞),增区间为(0,1).
(2)①由已知h(x)=lnx+bx,(x>0).
所以h$′(x)=\frac{1}{x}+b$,(x>0),
当b≥0时,显然h′(x)>0恒成立,此时函数h(x)在定义域内递增,h(x)至多有一个零点,不合题意.
当b<0时,令h′(x)=0得x=$-\frac{1}{b}$>0,令h′(x)>0得$0<x<-\frac{1}{b}$;令h′(x)<0得$x>-\frac{1}{b}$.
所以h(x)极大=h($-\frac{1}{b}$)=-ln(-b)-1>0,解得$-\frac{1}{e}<b<0$.
且x→0时,lnx<0,x→+∞时,lnx>0.
所以当$b∈(-\frac{1}{e},0)$时,h(x)有两个零点.
②证明:由题意得$\left\{\begin{array}{l}{ln{x}_{1}+b{x}_{1}=0}\\{ln{x}_{2}+b{x}_{2}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{{e}^{-b{x}_{1}}={x}_{1}①}\\{{e}^{-b{x}_{2}}={x}_{2}②}\end{array}\right.$,
①×②得${e}^{-b({x}_{1}+{x}_{2})}={x}_{1}{x}_{2}$.
因为x1,x2>0,
所以-b(x1+x2)>0,
所以${e}^{-b({x}_{1}+{x}_{2})}={x}_{1}{x}_{2}>1$,
因为0<-b<$\frac{1}{e}$,
所以e-b<1,
所以x1x2>${e}^{-2b\sqrt{{x}_{1}{x}_{2}}}$>${e}^{2\sqrt{{x}_{1}{x}_{2}}}$>e2,
所以$\frac{{{x}_{1}x}_{2}}{{e}^{2}}$>1.
点评 本题考查了导数和函数的单调性和极值的关系,以及函数的零点存在定理和不等式的证明,培养了学生的运算能力,化归能力,分类讨论的能力,属于难题.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨(¬q) | C. | (¬p)∧q | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | -2 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1-\sqrt{5}}{4}$,0) | B. | ($\frac{1-\sqrt{5}}{4}$,$\frac{\sqrt{5}-2}{2}$) | C. | [$\frac{9-9\sqrt{5}}{32}$,$\frac{\sqrt{5}-2}{2}$) | D. | [$\frac{9-9\sqrt{5}}{32}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
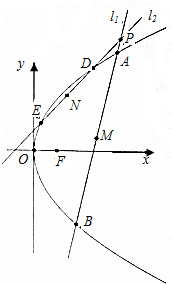 已知抛物线C:y2=2px(p>0)的焦点为F,定点P(3,4)到焦点F的距离为2$\sqrt{5}$且线段PF与抛物线C有公共点,过点P的动直线l1,l2的斜率分别为k1,k2,且满足k1+k2=4,若l1交抛物线C于A,B两点,l2交抛物线C于D,E两点,弦AB,DE的中点分别为M,N.
已知抛物线C:y2=2px(p>0)的焦点为F,定点P(3,4)到焦点F的距离为2$\sqrt{5}$且线段PF与抛物线C有公共点,过点P的动直线l1,l2的斜率分别为k1,k2,且满足k1+k2=4,若l1交抛物线C于A,B两点,l2交抛物线C于D,E两点,弦AB,DE的中点分别为M,N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,-1) | B. | (-1,0) | C. | (1,2) | D. | (3,6) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com