
| A. | (-3,-1) | B. | (-1,0) | C. | (1,2) | D. | (3,6) |
分析 求出函数f(x)的定义域,根据复合函数单调性的判断方法求出函数f(x)的减区间,由题意知区间E为f(x)减区间的子集,据此可得答案.
解答 解:给定区间E,对任意x1,x2∈E,当x1<x2时,总有f(x1)<f(x2),函数是增函数.
由x2-2x-3>0解得x<-1或x>3,
所以函数f(x)的定义域为(-∞,-1)∪(3,+∞),
因为y=$lo{g}_{\frac{2}{3}}x$递减函数,而t=x2-2x-3在(-∞,-1)上递减,在(3,+∞)上递增,
所以函数f(x)的减区间为(-∞,-1),增区间为(3,+∞),
由题意知,函数f(x)在区间E上单调递增,则E⊆(-∞,-1),
而(-3,-1)⊆(-∞,-1),
故选:A.
点评 本题考查复合函数单调性,判断复合函数单调性的方法是:“同增异减”,解决本题的关键是准确理解区间E的意义.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-4,+∞) | B. | (-2,+∞) | C. | [-4,-2) | D. | [-4,-2)∪(-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 48种 | B. | 24种 | C. | 20种 | D. | 12种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
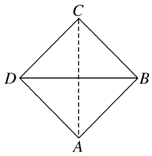 已知正四面体(所有棱长都相等的三棱锥)的俯视图如图所示,其中四边形ABCD是边长为$\sqrt{2}$cm的正方形,则这个正四面体的主视图的面积为( )cm2.
已知正四面体(所有棱长都相等的三棱锥)的俯视图如图所示,其中四边形ABCD是边长为$\sqrt{2}$cm的正方形,则这个正四面体的主视图的面积为( )cm2.| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
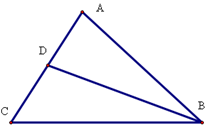 在△ABC中,角A、B、C所对的边分别为a,b,c,B=45°,AC=$\sqrt{5}$,cosC=$\frac{{\sqrt{5},}}{5}$,求
在△ABC中,角A、B、C所对的边分别为a,b,c,B=45°,AC=$\sqrt{5}$,cosC=$\frac{{\sqrt{5},}}{5}$,求查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com