
分析 (1)观察已知排列的数,依次正整数的个数是,1,2,4,8,…,分析得出是规律,根据规律求出第n行的最后一个数.
(2)由(1)得到第n行的第一个数,且此行一共有2 n-1个数,从而利用等差数列的求和公式即可计算第n行的各个数之和;
(3)由(1)可知第n行的最后一个数是2n-1,即可推断
(4)对于存在性问题,可先假设存在,即存在n使得S′=227-213-120,再利用(II)的结论,构建等式,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答 解:(1)由已知得出每行的正整数的个数是1,2,4,8,…,其规律:
1=21-1,
2=22-1,
4=23-1,
8=24-1,
…,
由此得出第n行的第一个数为:2n-1,共有2n-1个,
所以此表第n行的最后一个数是2n-1
(2)由(1)得到第n行的第一个数,且此行一共有2 n-1个数,从而利用等差数列的求和公式得:
第n行的各个数之和S=$\frac{{2}^{n-1}({2}^{n-1}+{2}^{n}-1)}{2}$=$\frac{3}{8}$•4n-$\frac{1}{4}$•2n=3×22n-3-2n-2,
(3)由(1)可知第n行的最后一个数是2n-1,
当n=11时,最后一个数字为1023,
当n=12时,最后一个数字为2047,
所以2010在第第12行,2010-1023=987,
故2010是第12行的第987个数;
(III)第n行起的连续10行的所有数之和S=$\frac{3}{8}$•4n(1+4+…+49)-$\frac{1}{4}$•2n=(1+2+…+29)
=2n-2(2n+19-2n-1-1023),
又227-213-120=23(224-210-15)
若存在n使得S′=227-213-120,
则2n-2(2n+19-2n-1-1023)=23(224-210-15)…(*)
所以n-2≥3,所以n≥5.n=5时,(*)式成立,
n>5时由(*)可得2n-5(2n+19-2n-1-1023)=224-210-15,
此等式左边偶数右边奇数,不成立.
所以满足条件的n=5.
点评 此题考查的知识点是等差数列与等比数列的综合、图形数字的变化类问题,同时考查学生分析归纳问题的能力,其关键是从每行的正整数个数1,2,4,8,…这列数找出规律解答.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b-a<b-c | B. | logab>logcb | C. | ab+cb<(a+c)b | D. | loga(c-b)>logc(a-b) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 常 喝 | 不常喝 | 总 计 | |
| 肥 胖 | 2 | ||
| 不肥胖 | 18 | ||
| 总 计 | 30 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
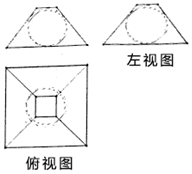 如图是某几何体挖去一部分后得到的三视图,其中主视图和左视图相同都是一个等腰梯形及它的内切圆,俯视图中有两个边长分别为2和8的正方形且图中的圆与主视图圆大小相等并且圆心为两个正方形的中心.问该几何体的体积是( )
如图是某几何体挖去一部分后得到的三视图,其中主视图和左视图相同都是一个等腰梯形及它的内切圆,俯视图中有两个边长分别为2和8的正方形且图中的圆与主视图圆大小相等并且圆心为两个正方形的中心.问该几何体的体积是( )| A. | $\frac{420-32π}{3}$ | B. | $\frac{336-32π}{3}$ | C. | $\frac{168-4π}{3}$ | D. | $\frac{168\sqrt{2}-64\sqrt{2}π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 推理的形式错误 | B. | 大前提是错误的 | C. | 小前提是错误的 | D. | 结论是正确的 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com