Question

9．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$，$\overrightarrow{d}$及实数x，y满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1，$\overrightarrow{c}$=$\overrightarrow{a}$+（x²-3）$\overrightarrow{b}$，$\overrightarrow{d}$=-y•$\overrightarrow{a}$+x•$\overrightarrow{b}$，若$\overrightarrow{a}$⊥$\overrightarrow{b}$，$\overrightarrow{c}$⊥$\overrightarrow{d}$，且|$\overrightarrow{c}$|≤$\sqrt{10}$．
（1）求y关于x的函数关系式y=f（x）及其定义域；
（2）若当x∈（1，$\sqrt{6}$）时，不等式f（x）≥mx+16恒成立，求实数m的取值范围．

Answer 1

分析 （1）由$\overrightarrow{c}•\overrightarrow{d}$=0整理得出f（x）的解析式，由|$\overrightarrow{c}$|≤$\sqrt{10}$列出不等式求出定义域；
（2）分别作出y=f（x）和y=mx+16的函数图象．根据图象关系得出m的范围．

解答 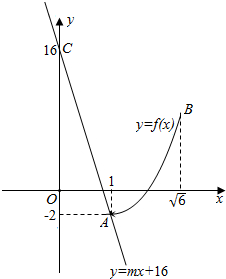解：（1）∵$\overrightarrow{a}$⊥$\overrightarrow{b}$，∴$\overrightarrow{a}•\overrightarrow{b}$=0，∵$\overrightarrow{c}$⊥$\overrightarrow{d}$，∴$\overrightarrow{c}•\overrightarrow{d}$=0，∴[$\overrightarrow{a}$+（x²-3）$\overrightarrow{b}$]•（-y•$\overrightarrow{a}$+x•$\overrightarrow{b}$）=0，即-y$\overrightarrow{a}$²+x（x²-3）$\overrightarrow{b}$²=0，
∵${\overrightarrow{a}}^{2}$=${\overrightarrow{b}}^{2}$=1，∴y=x（x²-3）=x³-3x．
∵|$\overrightarrow{c}$|≤$\sqrt{10}$，∴[$\overrightarrow{a}$+（x²-3）$\overrightarrow{b}$]²=1+（x²-3）²≤10，解得-$\sqrt{6}$≤x≤$\sqrt{6}$．
∴f（x）=x³-3x．定义域是[-$\sqrt{6}$，$\sqrt{6}$]．
（2）f′（x）=3x²-3，∵x∈（1，$\sqrt{6}$），∴f′（x）＞0，∴f（x）在（1，$\sqrt{6}$）上是增函数，
作出f（x）在（1，$\sqrt{6}$）上的函数图象如下：
令g（x）=mx+16，由图象可知当g（x）经过A（1，-2）时m取得最大值-18，
∴m≤-18．

点评 本题考查了平面向量的数量积运算，函数恒成立问题，借助函数图象可快速找到符合条件的m．