
���� ����ֱ��l�ļ����귽���Ǧ�cos��-��sin��-1=0�����û�����ʽ�ɵã�ֱ��l��ֱ�����귽�̣�����C�IJ���������$\left\{{\begin{array}{l}{x=cos��-1}\\{y=sin��}\end{array}}\right.$����Ϊ������������ƽ����ϵ�ɵã�����C����ͨ����
���� ����C���ԣ�-1��0��Բ�ģ���1Ϊ�뾶��Բ�����õ㵽ֱ�ߵľ��빫ʽ�ɵã�Բ�ĵ�ֱ��l�ľ���Ϊd��|MN|=$2\sqrt{{r}^{2}-{d}^{2}}$�����ɵó���PMN���������Сֵ��
��� �⣺����ֱ��l�ļ����귽���Ǧ�cos��-��sin��-1=0�����û�����ʽ�ɵã�ֱ��l��ֱ�����귽��Ϊx-y-1=0��
����C�IJ���������$\left\{{\begin{array}{l}{x=cos��-1}\\{y=sin��}\end{array}}\right.$����Ϊ������������ƽ����ϵ�ɵã�����C����ͨ����Ϊ��x+1��2+y2=1��
���� ����C���ԣ�-1��0��Բ�ģ���1Ϊ�뾶��Բ��
Բ�ĵ�ֱ��l�ľ���Ϊ$\frac{{|{-1-0-1}|}}{{\sqrt{2}}}=\sqrt{2}$��
��|MN|=$2\sqrt{{r}^{2}-{d}^{2}}$=$\sqrt{2}$�����ԡ�PMN���������Сֵ��$\frac{1}{2}��\sqrt{2}����\sqrt{2}-1��=1-\frac{{\sqrt{2}}}{2}$��
���� ���⿼���˼����귽�̻�Ϊֱ�����귽�̡��������̻�Ϊ��ͨ���̡��㵽ֱ�ߵľ��빫ʽ���ҳ���ʽ��������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����ʡ2014��ȫʡ������������ͳ�Ƶ�����ʾ��ȫʡ���������߷�����̬�ֲ�N��170.5.16���������꼶�����������ȡ50���������ߣ��������ֱ���ѧ������ȫ������175.5cm��187.5cm֮�䣬��������������·�ʽ�ֳ�6�飺�� һ��[157.5��162.5�����ڶ���[162.5��167.5�������� 6 �飨182.5��187.5]�����������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
����ʡ2014��ȫʡ������������ͳ�Ƶ�����ʾ��ȫʡ���������߷�����̬�ֲ�N��170.5.16���������꼶�����������ȡ50���������ߣ��������ֱ���ѧ������ȫ������175.5cm��187.5cm֮�䣬��������������·�ʽ�ֳ�6�飺�� һ��[157.5��162.5�����ڶ���[162.5��167.5�������� 6 �飨182.5��187.5]�����������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
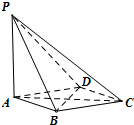 ��ͼ��������P-ABCD�У�PA��ƽ��ABCD������ABCD�����Σ�AB=2����BAD=60��
��ͼ��������P-ABCD�У�PA��ƽ��ABCD������ABCD�����Σ�AB=2����BAD=60���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{8}$ | B�� | $\frac{3}{8}$ | C�� | $\frac{5}{8}$ | D�� | $\frac{1}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
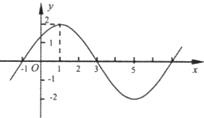 ��1����֪����$f��x��=Asin{����x+�գ�_{\;}}��A��0���أ�0��|��|��\frac{��}{2}��$��ͼ���һ������ͼ��ʾ������f��x���Ľ���ʽ��
��1����֪����$f��x��=Asin{����x+�գ�_{\;}}��A��0���أ�0��|��|��\frac{��}{2}��$��ͼ���һ������ͼ��ʾ������f��x���Ľ���ʽ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��7 | B�� | 6��14 | C�� | 3 | D�� | 7 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com