练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （2013•红桥区二模）已知集合 M={x||x+2|+|x﹣1|≤5}，N={x|a＜x＜6}，且M∩N=（﹣1，b]，则b﹣a=（ ）

    A.﹣3 B.﹣1 C.3 D.7

     

    C

    【解析】

    试题分析：解绝对值不等式求得 M={x|﹣3≤x≤2}，再由N={x|a＜x＜6}，且M∩N=（﹣1，b]，可得a=﹣1，b=2，从而求得b﹣a的值．

    【解析】
    由于|x+2|+|x﹣1|表示数轴上的x对应点到﹣2和1对应点的距离之和，

    而﹣3和2对应点到﹣2和1对应点的距离之和正好等于5，故由|x+2|+|x﹣1|≤5可得﹣3≤x≤2，

    ∴集合 M={x||x+2|+|x﹣1|≤5}={x|﹣3≤x≤2}．

    再由N={x|a＜x＜6}，且M∩N=（﹣1，b]，可得a=﹣1，b=2，b﹣a=3，

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.1二维形式柯西不等式练习卷（解析版） 题型：选择题

    已知a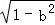+b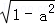=1，则以下成立的是（ ）

    A.a2+b2＞1 B.a2+b2=1 C.a2+b2＜1 D.a2b2=1

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.1比较法练习卷（解析版） 题型：填空题

    要证明“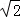+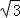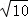＜”可选择的方法有以下几种，其中最合理的是 ．（填序号）

    ①反证法

    ②分析法

    ③综合法．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.1比较法练习卷（解析版） 题型：选择题

    若不等式（﹣1）na＜2+对任意n∈N*恒成立，则实数a的取值范围是（ ）

    A.[﹣2，） B.（﹣2，） C.[﹣3，） D.（﹣3，）

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 1.2绝对值不等式练习卷（解析版） 题型：填空题

    （2014•江西二模）不等式|2﹣x|+|x+1|≤a对任意x∈[0，5]恒成立的实数a的取值范围是 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 1.2绝对值不等式练习卷（解析版） 题型：选择题

    （2014•吉安二模）已知f（x）=|x﹣1|+|x+m|（m∈R），g（x）=2x﹣1，若m＞﹣1，x∈[﹣m，1]，不等式f（x）＜g（x）恒成立，则实数m的取值范围是（ ）

    A.（﹣1，﹣] B.（﹣1，﹣） C.（﹣∞，﹣] D.（﹣1，+∞）

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 1.2绝对值不等式练习卷（解析版） 题型：选择题

    （2014•南昌模拟）对任意x∈R，且x≠0，不等式|x+|＞|a﹣5|+1恒成立，则实数a的取值范围是（ ）

    A.（﹣∞，4）∪（6，+∞） B.（2，8） C.（3，5） D.（4，6）

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 1.1不等式练习卷（解析版） 题型：选择题

    （2014•浙江模拟）设正实数x，y满足x+y=1，则+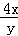的最小值为（ ）

    A.4 B.5 C.6 D.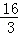

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-2 4.2特征向量的应用练习卷（解析版） 题型：解答题

    已知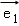=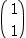是矩阵M=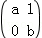属于特征值λ1=2的一个特征向量．

    （Ⅰ）求矩阵M；

    （Ⅱ）若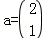，求M10a．

     

    查看答案和解析>>

    同步练习册答案