
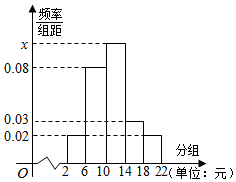
 某学校为了引导学生树立正确的消费观,对某班50名学生每天的零花钱(单位:元)进行了调查,将他们的零用钱分成5段[2,6),[6,10),[10,14),[14,18),[18,22),得到如下频率分布直方图.
某学校为了引导学生树立正确的消费观,对某班50名学生每天的零花钱(单位:元)进行了调查,将他们的零用钱分成5段[2,6),[6,10),[10,14),[14,18),[18,22),得到如下频率分布直方图.分析 (Ⅰ)由频率分布直方图中小矩形面积之和为1,能求出x=0.1,由此能估计此班50名同学每天零用钱的众数和平均数.
(Ⅱ)设事件A为这两人在[18,22)中恰有一人,由已知得在[14,18)内有6人,在[18,22)内有4人,由此能求出在[18,22)中恰有一人的概率.
解答 解:(Ⅰ)由图知五段的频率分别为0.08,0.3 2,4x,0.12,0.08,
∴0.08+0.3 2+4x+0.12+0.08=1解得x=0.1.
由图知众数的估计值为12,
平均数估计值为:
4×0.08+8×0.32+12×0.4+16×0.12+20×0.08=11.2.…(6分)
(Ⅱ)设事件A为这两人在[18,22)中恰有一人,
由已知得在[14,18)内有6人,在[18,22)内有4人,
从10人中取2人的结果有45种,事件A的结果有24种,
故在[18,22)中恰有一人的概率P(A)=$\frac{24}{45}$=$\frac{8}{15}$.…(12分)
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意频率分布直方图的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 250种 | B. | 450种 | C. | 270种 | D. | 540种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,$OC=90km,∠AOB=\frac{2π}{3},∠OCD=θ$,点O处为一雷达站,测控范围为一个圆形区域(含边界),雷达开机时测控半径r随时间t变化函数为r=3t$\sqrt{t}$km,且半径增大到81km时不再变化.一架无人侦察机从C点处开始沿CD方向飞行,其飞行速度为15km/min.
如图,$OC=90km,∠AOB=\frac{2π}{3},∠OCD=θ$,点O处为一雷达站,测控范围为一个圆形区域(含边界),雷达开机时测控半径r随时间t变化函数为r=3t$\sqrt{t}$km,且半径增大到81km时不再变化.一架无人侦察机从C点处开始沿CD方向飞行,其飞行速度为15km/min.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{36}$ | B. | $\frac{1}{18}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A | B | |
| C | D | |
| E | ||
| A. | 500种 | B. | 520种 | C. | 540种 | D. | 560种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com