
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据向量共线定理结合充分必要条件判断即可.
解答 解:已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$均为非零向量,
则$\overrightarrow{a}$∥$\overrightarrow{c}$,则$\overrightarrow{b}$•$\overrightarrow{c}$≠0,∴$\overrightarrow{a}$=$\frac{\overrightarrow{a}•\overrightarrow{b}}{\overrightarrow{b}•\overrightarrow{c}}$•$\overrightarrow{c}$,即($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$=$\overrightarrow{a}$•($\overrightarrow{b}$•$\overrightarrow{c}$),是充分条件,
若($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$=$\overrightarrow{a}$•($\overrightarrow{b}$•$\overrightarrow{c}$),$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$均为非零向量,则$\overrightarrow{b}$•$\overrightarrow{c}$≠0,
∴$\overrightarrow{a}$=$\frac{\overrightarrow{a}•\overrightarrow{b}}{\overrightarrow{b}•\overrightarrow{c}}$•$\overrightarrow{c}$,∴$\overrightarrow{a}$∥$\overrightarrow{b}$,是必要条件,
故选:C.
点评 本题考查了充分必要条件,考查共线向量问题,是一道基础题.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | 1008 | C. | 22016 | D. | 21008 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 20,2 | B. | 24,4 | C. | 25,2 | D. | 25,4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
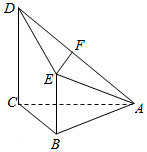 如图,四棱锥A-BCDE中,AB=BCC,BE=$\frac{1}{2}$CD.CD⊥面ABC,BE∥CD,F为AD的中点.
如图,四棱锥A-BCDE中,AB=BCC,BE=$\frac{1}{2}$CD.CD⊥面ABC,BE∥CD,F为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
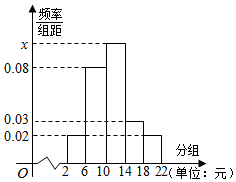 某学校为了引导学生树立正确的消费观,对某班50名学生每天的零花钱(单位:元)进行了调查,将他们的零用钱分成5段[2,6),[6,10),[10,14),[14,18),[18,22),得到如下频率分布直方图.
某学校为了引导学生树立正确的消费观,对某班50名学生每天的零花钱(单位:元)进行了调查,将他们的零用钱分成5段[2,6),[6,10),[10,14),[14,18),[18,22),得到如下频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com