

| A. | 20,2 | B. | 24,4 | C. | 25,2 | D. | 25,4 |
分析 先由频率分布直方图求出[50,60)的频率,结合茎叶图中得分在[50,60)的人数求得本次考试的总人数,根据频率分布直方图可知[90,100]内的人数与[50,60)的人数一样.
解答 解:由频率分布直方图可知,组距为10,[50,60)的频率为0.008×10=0.08,
由茎叶图可知[50,60)的人数为2,设参加本次考试的总人数为N,则,所以N=$\frac{2}{0.08}$=25,
根据频率分布直方图可知[90,100]内的人数与[50,60)的人数一样,都是2,
故选:C.
点评 本题考查了茎叶图和频率分布直方图,茎叶图中,茎在高位,叶在低位,频率分布直方图中要注意纵轴的单位,同时掌握频率和等于1,此题是基础题.


科目:高中数学 来源: 题型:填空题
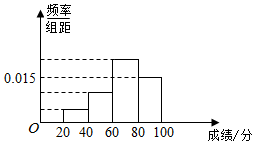 北京市某校组织学生惨叫英语测试,某班50人的成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),已知前3组的人数依次构成等比数列,第2组、第4组、第3组的人数依次构成等差数列,则及格(大于等于60分)的人数是35.
北京市某校组织学生惨叫英语测试,某班50人的成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),已知前3组的人数依次构成等比数列,第2组、第4组、第3组的人数依次构成等差数列,则及格(大于等于60分)的人数是35.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| A | B | C | D | E | |
| 语文 | 119 | 121 | 123 | 125 | 134 |
| 数学 | 123 | 141 | 118 | 122 | 132 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| A. | 18 | B. | 36 | C. | 72 | D. | 108 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com