
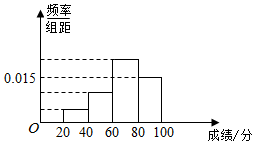
 北京市某校组织学生惨叫英语测试,某班50人的成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),已知前3组的人数依次构成等比数列,第2组、第4组、第3组的人数依次构成等差数列,则及格(大于等于60分)的人数是35.
北京市某校组织学生惨叫英语测试,某班50人的成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),已知前3组的人数依次构成等比数列,第2组、第4组、第3组的人数依次构成等差数列,则及格(大于等于60分)的人数是35. 分析 根据前3组的人数依次构成等比数列,第2组、第4组、第3组的人数依次构成等差数列,得到a+aq+aq2=0.035,①,aq+aq2=0.03,②,解得求出a,q的值,即可求出及格(大于等于60分)的人数.
解答 解:由题意,前3组的$\frac{频率}{组距}$也依次构成等比数列,设前3组的$\frac{频率}{组距}$也依次a,aq,aq2,(a>0,q>0),则a+aq+aq2=$\frac{1}{20}$-0.015=0.035,①,
且由题意,可知第2组、第4组、第3组的$\frac{频率}{组距}$依次构成等差数列,得aq+aq2=0.015×2=0.03,②,
由①②,得a=0.005,再代入②中,得到0.005(q+q2)=0.03,
解得q=2或q=-3(舍去),
因为大于等于60分的频率为20×(0.015+0.02)=0.7,
所以及格(大于等于60分)的人数是50×0.7=35,
故答案为:35.
点评 本题考查了等差数列和等比数列的定义以及频率分布直方图,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 成等差数列 | B. | 成等比数列 | ||
| C. | 各项倒数成等差数列 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 空气质量指数 | 污染程度 |
| 小于100 | 优良 |
| 大于100且小于150 | 轻度 |
| 大于150且小于200 | 中度 |
| 大于200且小于300 | 重度 |
| 大于300且小于500 | 严重 |
| 大于500 | 爆表 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?n∈N*,$\frac{1}{n}$≤$\frac{1}{n+1}$ | B. | ?n∈N*,$\frac{1}{n}$<$\frac{1}{n+1}$ | ||
| C. | ?n∈N*,$\frac{1}{{n}_{0}}$≤$\frac{1}{{n}_{0}+1}$ | D. | ?n0∈N*,$\frac{1}{{n}_{0}}$<$\frac{1}{{n}_{0}+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | 1008 | C. | 22016 | D. | 21008 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 20,2 | B. | 24,4 | C. | 25,2 | D. | 25,4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com