
分析 对于$\frac{0}{0}$的式子求极限问题,一般运用洛必达法则,
解答 解:(1)为$\frac{0}{0}$式,利用洛必达法则:$\underset{lim}{n→1}\frac{2x}{1}=2$
(2)为$\frac{0}{0}$式,利用洛必达法则:原式=$\underset{lim}{n→-2}\frac{1}{2x+1}=-\frac{1}{3}$
(3)为$\frac{0}{0}$式,利用洛必达法则:原式=$\underset{lim}{n→-1}\frac{2x+1}{2x-2}=\frac{1}{4}$
(4)将x=2代入得$\underset{lim}{n→2}=\frac{\sqrt{2+2}-1}{2}=\frac{1}{2}$
点评 本题主要考察,对于$\frac{0}{0}$型的式子求极限问题,一般采用洛必达法则,属于基础题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
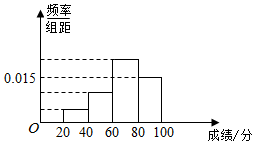 北京市某校组织学生惨叫英语测试,某班50人的成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),已知前3组的人数依次构成等比数列,第2组、第4组、第3组的人数依次构成等差数列,则及格(大于等于60分)的人数是35.
北京市某校组织学生惨叫英语测试,某班50人的成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),已知前3组的人数依次构成等比数列,第2组、第4组、第3组的人数依次构成等差数列,则及格(大于等于60分)的人数是35.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com