
分析 设等差数列{an}的公差为d,等比数列{bn}的公比为q,化简an+3an+1=q(an+2)2,从而可得an+3a3n+1=(an+2)3an,从而化简可得and=0,从而求得.
解答 解:设等差数列{an}的公差为d,等比数列{bn}的公比为q,
∵$\frac{{a}_{n+1}}{{a}_{n}}$=bn,∴$\frac{{a}_{n+2}}{{a}_{n+1}}$=bn+1,
∴$\frac{{a}_{n+2}{a}_{n}}{{(a}_{n+1})^{2}}$=q,∴an+2an=q(an+1)2,
∴an+3an+1=q(an+2)2,
∴$\frac{{a}_{n+3}{a}_{n+1}}{{a}_{n+2}{a}_{n}}$=$\frac{{{a}^{2}}_{n+2}}{{{a}^{2}}_{n+1}}$,
即an+3a3n+1=(an+2)3an,
即(an+3d)(an+d)3=(an+2d)3an,
化简可得,and=0,
∵an≠0,∴d=0,
故数列{an}是常数列,
故bn=$\frac{{a}_{n+1}}{{a}_{n}}$=1,
故答案为:bn=1.
点评 本题考查了学生的化简运算能力及整体思想与转化思想的应用,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 216 | B. | 224 | C. | $\frac{6056}{27}$ | D. | 26 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}+1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
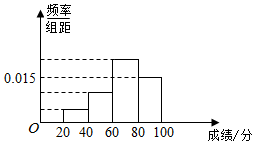 北京市某校组织学生惨叫英语测试,某班50人的成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),已知前3组的人数依次构成等比数列,第2组、第4组、第3组的人数依次构成等差数列,则及格(大于等于60分)的人数是35.
北京市某校组织学生惨叫英语测试,某班50人的成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),已知前3组的人数依次构成等比数列,第2组、第4组、第3组的人数依次构成等差数列,则及格(大于等于60分)的人数是35.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com