
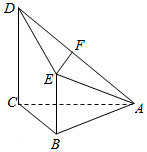
 如图,四棱锥A-BCDE中,AB=BCC,BE=$\frac{1}{2}$CD.CD⊥面ABC,BE∥CD,F为AD的中点.
如图,四棱锥A-BCDE中,AB=BCC,BE=$\frac{1}{2}$CD.CD⊥面ABC,BE∥CD,F为AD的中点.分析 (1)取AC中点M,连结FM,BM,利用中位线定理和平行公理证明四边形EFMB是平行四边形,得出EF∥BM,故而EF∥平面ABC;
(2)由CD⊥平面ABC得CD⊥BM,由AB=BC得AC⊥BM,故BM⊥平面ACD,于是EF⊥平面ACD,故而平面ADE⊥平面ACD.
解答 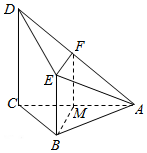 证明:(1取AC中点M,连结FM,BM,
证明:(1取AC中点M,连结FM,BM,
∵F,M分别是AD,AC的中点,
∴FM$\stackrel{∥}{=}$$\frac{1}{2}$CD,∵BE$\stackrel{∥}{=}\frac{1}{2}CD$,
∴四边形EFMB是平行四边形,
∴EF∥BM,∵EF?平面ABC,BM?平面ABC,
∴EF∥平面ABC.
(2)∵AB=BC,M是AC的中点,
∴BM⊥AC,
∵CD⊥平面ABC,BM?平面ABC,
∴CD⊥BM
又CD?平面ACD,AC?平面ACD,CD∩AC=C,
∴BM⊥平面ACD,∵EF∥BM,
∴EF⊥平面ACD,∵EF?平面ADE,
∴平面ADE⊥平面ACD.
点评 本题考查了线面平行,面面垂直的判定,线面垂直的性质,构造平行线是解决问题的关键,属于中档题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:填空题
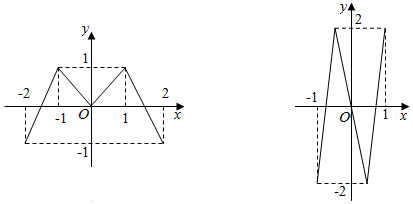
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| A. | 18 | B. | 36 | C. | 72 | D. | 108 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,$OC=90km,∠AOB=\frac{2π}{3},∠OCD=θ$,点O处为一雷达站,测控范围为一个圆形区域(含边界),雷达开机时测控半径r随时间t变化函数为r=3t$\sqrt{t}$km,且半径增大到81km时不再变化.一架无人侦察机从C点处开始沿CD方向飞行,其飞行速度为15km/min.
如图,$OC=90km,∠AOB=\frac{2π}{3},∠OCD=θ$,点O处为一雷达站,测控范围为一个圆形区域(含边界),雷达开机时测控半径r随时间t变化函数为r=3t$\sqrt{t}$km,且半径增大到81km时不再变化.一架无人侦察机从C点处开始沿CD方向飞行,其飞行速度为15km/min.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=2sin(x+$\frac{π}{6}$) | B. | f(x)=2sin(x+$\frac{π}{3}$) | C. | f(x)=2sin(2x+$\frac{π}{6}$) | D. | f(x)=2sin(2x+$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com