
分析 利用同角三角函数间的基本关系可求得sinθ-cosθ=$\frac{7}{5}$,从而可求得sinθ与cosθ,继而可得答案.
解答 解:∵sinβ+cosβ=$\frac{1}{5}$,①
∴两边平方可得:1+sin2β=$\frac{1}{25}$,
∴sin2β=-$\frac{24}{25}$,又0≤β≤π,
∴sinβ>0,cosβ<0,
∴(sinβ-cosβ)2=1-sin2β=$\frac{49}{25}$,
∴sinβ-cosβ=$\frac{7}{5}$,②
由①②得:sinβ=$\frac{4}{5}$,cosβ=-$\frac{3}{5}$.
∴tanβ=-$\frac{4}{3}$.
故答案为:-$\frac{4}{3}$.
点评 本题主要考查了三角函数的恒等变换及化简求值.考查了考生对三角函数基础公式的熟练应用,属于中档题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
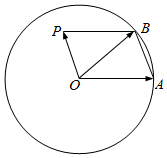 已知点A、B为单位圆O上的两点,点P为单位圆0所在平面内的一点,且$\overrightarrow{OA}$与$\overrightarrow{OB}$不共线.
已知点A、B为单位圆O上的两点,点P为单位圆0所在平面内的一点,且$\overrightarrow{OA}$与$\overrightarrow{OB}$不共线.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
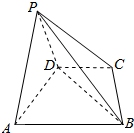 在四棱锥P-ABCD 中,△PAD 为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC=$\frac{1}{2}$AB=2,且平面PAD⊥平面ABCD.
在四棱锥P-ABCD 中,△PAD 为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC=$\frac{1}{2}$AB=2,且平面PAD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com