
分析 利用取值、作差、变形、判断符号、下结论这五步进行证明,主要利用通分和提取公因式进行变形.
解答 设任意的x1,x2∈(-∞,0),且x1<x2,
则f(x1)-f(x2)
=(x1-$\frac{1}{{x}_{1}}$)-(x2-$\frac{1}{{x}_{2}}$)
=(x1-x2)+($\frac{1}{{x}_{2}}$-$\frac{1}{{x}_{1}}$)
=(x1-x2)+$\frac{{x}_{1}{-x}_{2}}{{{x}_{1}x}_{2}}$
=(x1-x2)(1+$\frac{1}{{{x}_{1}x}_{2}}$)
=(x1-x2)•$\frac{{{x}_{1}x}_{2}+1}{{{x}_{1}x}_{2}}$,
∵x1<0,x2<0,且x1<x2,
∴x1-x2<0,x1x2>0,
∴f(x1)-f(x2)<0,
即f(x1)<f(x2),
∴f(x)在(-∞,0)上是增函数.
点评 本题主要考查函数单调性的判断和证明,利用定义法和导数法是解决函数单调性的基本方法.要求熟练掌握常见证明函数单调性的方法.属于基础题.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
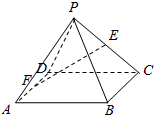 如图,四棱锥P-ABCD中,ABCD为矩形,面PDC⊥面ABCD,∠DPC=90°,E,F 分别为PC,AD的中点.
如图,四棱锥P-ABCD中,ABCD为矩形,面PDC⊥面ABCD,∠DPC=90°,E,F 分别为PC,AD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com