
分析 根据题意,得出函数y=x+$\frac{a}{x}$(a>0)在(0,$\sqrt{a}$]上是减函数,在[$\sqrt{a}$,+∞)上是增函数;
利用导数大于0或小于0证明函数y=f(x)的单调性即可.
解答 解:根据题意,得;
函数y=x+$\frac{a}{x}$(a>0)在(0,$\sqrt{a}$]上是减函数,在[$\sqrt{a}$,+∞)上是增函数;
证明如下:∵y=f(x)=x+$\frac{a}{x}$,
∴f′(x)=1-$\frac{a}{{x}^{2}}$,
令f′(x)=0,
解得x=±$\sqrt{a}$;
∴当0<x≤$\sqrt{a}$时,f′(x)≤0,f(x)是减函数;
x≥$\sqrt{a}$时,f′(x)≥0,f(x)是增函数;
综上,函数f(x)在(0,$\sqrt{a}$]上是减函数,在[$\sqrt{a}$,+∞)上是增函数.
点评 本题考查了判断函数的单调性问题,解题时可以利用导数来判断和证明函数的单调性问题,是基础题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
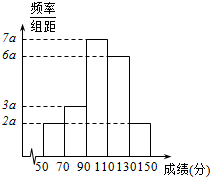 贵阳市某数学教师从他所教的2015届高三(X)班与高三(Y)班学生的高考数学成绩中,随机抽取20名学生的成绩绘制成频率分布直方图,如图所示.
贵阳市某数学教师从他所教的2015届高三(X)班与高三(Y)班学生的高考数学成绩中,随机抽取20名学生的成绩绘制成频率分布直方图,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com