
分析 由向量的三角形法则,可得①正确;运用直线方程和抛物线的方程联立,运用韦达定理和向量共线的条件,化简整理,即可判断②正确;运用向量的数量积的坐标表示,以及韦达定理,即可判断③正确;运用抛物线的定义以及以AB为直径的圆的半径与梯形ACDB的中位线长相等,可得该圆与CD相切,即可判断④不正确.
解答 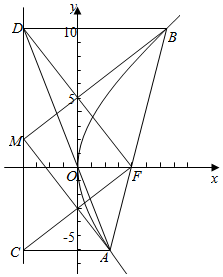 解:对于①,由$\overrightarrow{AC}$+$\overrightarrow{CD}$=$\overrightarrow{AD}$=$\overrightarrow{BD}$-$\overrightarrow{BA}$,可得①正确;
解:对于①,由$\overrightarrow{AC}$+$\overrightarrow{CD}$=$\overrightarrow{AD}$=$\overrightarrow{BD}$-$\overrightarrow{BA}$,可得①正确;
对于②,设A(x1,y1),B(x2,y2),可得C(-$\frac{p}{2}$,y1),D(-$\frac{p}{2}$,y2),
又kOA=$\frac{{y}_{1}}{{x}_{1}}$=$\frac{2p}{{y}_{1}}$,kAD=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}+\frac{p}{2}}$,设直线AB方程为x=my+$\frac{p}{2}$.
代入抛物线的方程,可得y2-2pmy-p2=0,
可得y1y2=-p2,即有y1(y1-y2)=y12-y1y2=2px1+p2,
则kOA=kAD,即有存在λ∈R,使得$\overrightarrow{AD}=λ\overrightarrow{AO}$成立,则②正确;
对于③,$\overrightarrow{FC}$•$\overrightarrow{FD}$=(-p,y1)•(-p,y2)=y1y2+p2=0,可得③正确;
对于④,由抛物线的定义可得|AB|=|AC|+|BD|,
可得以AB为直径的圆的半径与梯形ACDB的中位线长相等,
即有该圆与CD相切,设切点为M,即有AM⊥BM,则$\overrightarrow{AM}•\overrightarrow{BM}$=0,
则④不正确.
故答案为:①②③.
点评 本题考查抛物线的定义、方程和性质,同时考查向量的加减和数量积运算,考查直线方程和抛物线的方程联立,运用韦达定理,考查运算和推理能力,属于中档题.


 新课标同步训练系列答案
新课标同步训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m=9 | B. | m>9或0<m<1 | C. | m>9 | D. | 0<m<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
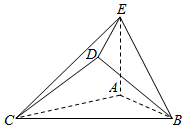 在如图所示的几何体中,已知△BCD是等腰直角三角形且BD=CD,AB=BC=AC=2,AE=1,AE⊥平面ABC,平面BCD⊥平面ABC.
在如图所示的几何体中,已知△BCD是等腰直角三角形且BD=CD,AB=BC=AC=2,AE=1,AE⊥平面ABC,平面BCD⊥平面ABC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com