
分析 (1)根据向量的数量积公式,计算即可,
(2)根据向量的夹角公式计算即可.
解答 解:(1)由题意:${|{\overrightarrow a-\overrightarrow b}|^2}=7⇒{\overrightarrow a^2}-2\overrightarrow a•\overrightarrow b+{\overrightarrow b^2}=7$,
则${1^2}-2\overrightarrow a•\overrightarrow b+4=7⇒\overrightarrow a•\overrightarrow b=-1$,
(2)$(\overrightarrow a-\overrightarrow b)(\overrightarrow a+\overrightarrow b)={\overrightarrow a^2}-{\overrightarrow b^2}=1-4=-3$,
$|{\overrightarrow a+\overrightarrow b}|=\sqrt{{{\overrightarrow a}^2}+2\overrightarrow a•\overrightarrow b+{{\overrightarrow b}^2}}=\sqrt{1+(-2)+4}=\sqrt{3}$,
设$\overrightarrow a-\overrightarrow b$与$\overrightarrow a+\overrightarrow b$的夹角为α,则$cosα=\frac{(\overrightarrow a-\overrightarrow b)(\overrightarrow a+\overrightarrow b)}{{|{\overrightarrow a-\overrightarrow b}|•|{\overrightarrow a+\overrightarrow b}|}}=\frac{-3}{{\sqrt{7}•\sqrt{3}}}=-\frac{{\sqrt{21}}}{7}$.
点评 本题考查了向量的数量积和向量的夹角公式,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
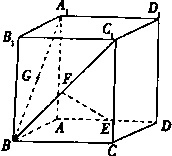 如图,在单位正方体A1B1C1D1-ABCD中,E,F,G分别是AD,BC1,A1B的中点.
如图,在单位正方体A1B1C1D1-ABCD中,E,F,G分别是AD,BC1,A1B的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M={2,3},S={(2,3)} | |
| B. | M={π},S={3.14} | |
| C. | M={0},S=∅ | |
| D. | M={1,2,3,…,n-1,n},S={前n个非零自然数} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}-1}}{2}$ | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $-\frac{{\sqrt{2}}}{2}$ | C. | $\frac{3}{5}$ | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{(n+1)(n+2)}{2}$ | B. | $\frac{n(n+1)}{2}$ | C. | $\frac{n}{n+1}$ | D. | $\frac{n}{n+2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com