Question

12．已知函数f（x）=xlnx，且0＜x₁＜x₂，给出下列命题：
①$\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＜1
②x₂f（x₁）＜x₁f（x₂）
③当lnx＞-1时，x₁f（x₁）+x₂f（x₂）＞2x₂f（x₁）
④x₁+f（x₁）＜x₂+f（x₂）
其中正确的命题序号是②③．

Answer 1

分析 根据条件分别构造不同的函数，求函数的导数，利用函数单调性和导数之间的关系进行判断即可．

解答 解：f′（x）=lnx+1，
x∈（0，$\frac{1}{e}$）时，f′（x）＜0，∴f（x）在（0，$\frac{1}{e}$）单调递减，
x∈（$\frac{1}{e}$，+∞），f′（x）＞0，．∴f（x）在（$\frac{1}{e}$，+∞）上单调递增．
①令g（x）=f（x）-x=xlnx-x，
则g′（x）=lnx，设x₁，x₂∈（1，+∞），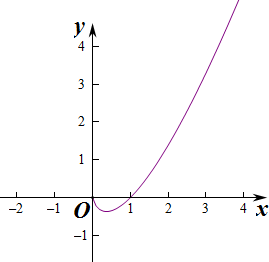
则g′（x）＞0，∴函数g（x）在（1，+∞）上是增函数，
∴由x₂＞x₁得g（x₂）＞g（x₁）；
∴f（x₂）-x₂＞f（x₁）-x₁，∴$\frac{{f（{x_1}）-f（{x_2}）}}{{{x_1}-{x_2}}}$＞1；故①错误；
②令g（x）=$\frac{f（x）}{x}$=lnx，则g′（x）=$\frac{1}{x}$，（0，+∞）上函数单调递增，
∵x₂＞x₁＞0，∴g（x₂）＞g（x₁），∴x₂•f（x₁）＜x₁•f（x₂），即②正确，
③当lnx₁＞-1时，f（x）单调递增，
∴x₁•f（x₁）+x₂•f（x₂）-2x₂f（x₁）=x₁[f（x₁）-f（x₂）]+x₂[f（x₂）-f（x₁）]=（x₁-x₂）[f（x₁）-f（x₂）]＞0
∴x₁•f（x₁）+x₂•f（x₂）＞x₁•f（x₂）+x₂f（x₁），
∵x₂•f（x₁）＜x₁•f（x₂），
利用不等式的传递性可以得到x₁•f（x₁）+x₂•f（x₂）＞2x₂f（x₁），故③正确．
④令h（x）=f（x）+x=xlnx+x，则h′（x）=lnx+2，
∴x∈（0，$\frac{1}{{e}^{2}}$）时，h′（x）＜0，
∴函数h（x）在（0，$\frac{1}{{e}^{2}}$）上单调递减，
设x₁，x₂∈（0，$\frac{1}{{e}^{2}}$），所以由x₁＜x₂得h（x₁）＞h（x₂），
∴f（x₁）+x₁＞f（x₂）+x₂，故④错误；
故答案为：②③

点评 本题主要考查命题的真假判断，在求解中用到了利用导数判断函数的单调性，并用到了函数单调性的定义．需要学习掌握的是构造函数的办法，综合性较强，有一定的难度．