练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E、F分别为弦AB与弦AC上的点,且BC·AE=DC·AF,B、E、F、C四点共圆.

    (1)证明:CA是△ABC外接圆的直径;

    (2)若DB=BE=EA,求过B、E、F、C四点的圆的面积与△ABC外接圆面积的比值.


     (1)证明:因为CD为△ABC外接圆的切线,所以∠DCB=∠A,由题设知=,故△CDB∽△AEF,

    所以∠DBC=∠EFA.

    因为B,E,F,C四点共圆,

    所以∠CFE=∠DBC,故∠EFA=∠CFE=90°.

    所以∠CBA=90°,因此CA是△ABC外接圆的直径.

    (2)解:连接CE,因为∠CBE=90°,

    所以过B,E,F,C四点的圆的直径为CE.

    由DB=BE,有CE=DC.

    又BC2=DB·BA=2DB2,

    所以CA2=4DB2+BC2=6DB2.

    而CE2=DC2=DB·DA=3DB2,

    故过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值为.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知抛物线关于x轴对称,它的顶点在坐标原点O,并且经过点M(2,y0).若点M到该抛物线焦点的距离为3,则|OM|等于(　　)

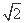    (A)2    (B)2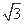  (C)4         (D)2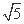

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若实数a,b,c满足2a+2b=2a+b,2a+2b+2c=2a+b+c,则c的最大值是　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f(x)=x+ (x>2)在x=a处取最小值,则a等于(　　)

    (A)1+   (B)1+    (C)3    (D)4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F,若AB=6,AE=1,则DF·DB=　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示,PC与圆O相切于点C,直线PO交圆O于A,B两点,弦CD垂直AB于E,则下面结论中,错误的结论是(　　)

    (A)△BEC∽△DEA

    (B)∠ACE=∠ACP

    (C)DE2=OE·EP

    (D)PC2=PA·AB

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,已知△ABC中的两条角平分线AD和CE相交于H,∠B=60°,F在AC上,且AE=AF.

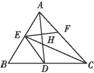
    (1)证明:B,D,H,E四点共圆;

    (2)证明:CE平分∠DEF.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设当x=θ时,函数f(x)=sin x-2cos x取得最大值,则cos θ=　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设P为直线y=x与双曲线-=1(a>0,b>0)左支的交点,F1是左焦点,PF1垂直于x轴,则双曲线的离心率e=　　　　. 

    查看答案和解析>>

    同步练习册答案