练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图,已知△ABC中的两条角平分线AD和CE相交于H,∠B=60°,F在AC上,且AE=AF.

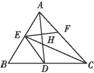
    (1)证明:B,D,H,E四点共圆;

    (2)证明:CE平分∠DEF.


    证明:(1)在△ABC中,∵∠B=60°,

    ∴∠BAC+∠BCA=120°.

    ∵AD,CE是角平分线,

    ∴∠HAC+∠HCA=60°,∴∠AHC=120°.

    ∴∠EHD=∠AHC=120°.

    ∵∠EBD+∠EHD=180°,

    ∴B,D,H,E四点共圆.

    (2)如图所示,连结BH,

    则BH为∠ABC的平分线,

    得∠HBD=30°.

    由(1)知B,D,H,E四点共圆,

    ∴∠CED=∠HBD=30°.

    又∠AEH=∠EBD=60°,AE=AF,AH平分∠EAF,

    ∴EF⊥AD.可得∠CEF=30°.

    ∴CE平分∠DEF.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知点A(2,0),抛物线C:x2=4y的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N,则|FM|∶|MN|等于(　　)

    (A)2∶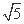     (B)1∶2        (C)1∶ 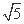    (D)1∶3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    双曲线-=1(a>0,b>0)的离心率为2,则的最小值为(　　)

    (A)    (B) (C)2    (D)1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E、F分别为弦AB与弦AC上的点,且BC·AE=DC·AF,B、E、F、C四点共圆.

    (1)证明:CA是△ABC外接圆的直径;

    (2)若DB=BE=EA,求过B、E、F、C四点的圆的面积与△ABC外接圆面积的比值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示,在正△ABC中,点D,E分别在边AC, AB上,且AD=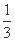AC,

     AE= AB,BD,CE相交于点F.

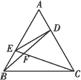
    (1)求证:A,E,F,D四点共圆;

    (2)若正△ABC的边长为2,求A,E,F,D所在圆的半径.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若P=+,Q=+(a≥0),则P、Q的大小关系是(　　)

    (A)P>Q  (B)P=Q

    (C)P<Q  (D)由a的取值确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    凸函数的性质定理:如果函数f(x)在区间D上是凸函数,则对于区间D内的任意x1,x2,…,xn,有≤f,已知函数y=sin x在区间

    (0,π)上是凸函数,则在△ABC中,sin A+sin B+sin C的最大值为　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y=sin2x+2cos x(≤x≤)的最大值与最小值分别为(　　)

    (A)最大值为,最小值为-

    (B)最大值为,最小值为-2

    (C)最大值为2,最小值为-

    (D)最大值为2,最小值为-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在平面直角坐标系xOy中,若双曲线-=1的离心率为,则m的值为　　　　. 

    查看答案和解析>>

    同步练习册答案