
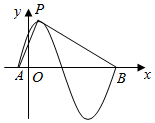
 函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,记∠APB=θ,则sin2θ的值是$\frac{16}{65}$.
函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,记∠APB=θ,则sin2θ的值是$\frac{16}{65}$. 分析 由题意,|AB|=2,P是图象的最高点,故P是纵坐标为1,设∠BAP=α,∠PBA=β,那么:θ=π-(α+β),过P作AB的垂线.即可求sinα,sinβ,cosα,cosβ,从而求sin2θ的值.
解答 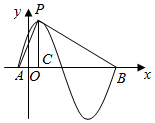 解:由题意,函数y=sin(πx+φ),T=$\frac{2π}{π}=2$,∴|AB|=2,
解:由题意,函数y=sin(πx+φ),T=$\frac{2π}{π}=2$,∴|AB|=2,
P是图象的最高点,故P是纵坐标为1,设∠BAP=α,∠PBA=β,那么:θ=π-(α+β),过P作AB的垂线交于C,|AC|=$\frac{1}{4}T=\frac{1}{2}$,|AP|=$\frac{\sqrt{5}}{2}$,|PC|=1,
那么:sinα=$\frac{|PC|}{|AP|}=\frac{2\sqrt{5}}{5}$,cosα=$\frac{\sqrt{5}}{5}$,
|BC|=$\frac{3}{4}T=\frac{3}{2}$,|PB|=$\frac{\sqrt{13}}{2}$,
那么:sinβ=$\frac{2\sqrt{13}}{13}$,cosβ=$\frac{3\sqrt{13}}{13}$,
则:sin2θ=2sinθcosθ=-2sin(α+β)cos(α+β)
=-2(sinαcosβ+cosαsinβ)(cosαcosβ-sinαsinβ)
=$\frac{16}{65}$,
故答案为:$\frac{16}{65}$.
点评 本题考查了三角函数图象及性质的运用和计算能力,属于中档题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{9}$ | B. | $\frac{9}{4}$ | C. | $-\frac{4}{9}$ | D. | $-\frac{9}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c<d | B. | a<c<d<b | C. | b<a<c<d | D. | c<b<a<d |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {x|x<-1} | C. | {x|x>1} | D. | {x|x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在△ABC中,角A,B,C所对的边分别为a,b,c,且a2+c2=b2-ac.
在△ABC中,角A,B,C所对的边分别为a,b,c,且a2+c2=b2-ac.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com