
【题目】在四棱锥A﹣BCDE中,底面BCDE为平行四边形,平面ABE⊥平面BCDE,AB=AE,DB=DE,∠BAE=∠BDE=90°
(1)求异面直线AB与DE所成角的大小;
(2)求二面角B﹣AE﹣C的余弦值.
【答案】
(1)解:设BE的中点为O,连结AO,DO,
∵AB=AE,BO=OE,∴AO⊥BE,同理DO⊥BE,
又∵平面ABE⊥平面BCDE,
平面ABE∩平面BCDE=BE,
∴AO⊥平面BCDE,
由题意,BE2=2AB2=2DB2,
∴AB=BD=DE=AE,
设AB=1,以B为原点,以BC为x轴,BD为y轴,
建立如图所示的空间直角坐标系,
则B(0,0,0),C(1,0,0),D(0,1,0),
E(﹣1,1,0),A(﹣ ![]() ,
, ![]() ,
, ![]() ),
),
则 ![]() =(
=( ![]() ),
), ![]() =(﹣1,0,0),
=(﹣1,0,0),
∵cos< ![]() ,
, ![]() >=
>= 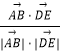 =
=  =﹣
=﹣ ![]() ,
,
∴ ![]() 与
与 ![]() 的夹角为120°,
的夹角为120°,
异面直线AB与DE所成角为60°.
(2)解:设平面ACE的法向量 ![]() =(x,y,z),
=(x,y,z),
![]() =(
=( ![]() ),
), ![]() =(﹣1,1,0),
=(﹣1,1,0),
则  ,取x=1,得
,取x=1,得 ![]() =(1,1,0),
=(1,1,0),
设平面ABE的法向量为 ![]() =(a,b,c),
=(a,b,c),
![]() =(
=( ![]() ),
), ![]() ,
,
则  ,取a=1,得
,取a=1,得 ![]() =(1,2,
=(1,2, ![]() ),
),
设二面角B﹣AE﹣C的平面角为θ,
cosθ=|cos< ![]() >|=
>|= ![]() =
= ![]() .
.
∴二面角B﹣AE﹣C的余弦值为 ![]() .
.

【解析】(1)设BE的中点为O,连结AO,DO,由已知得AO⊥BE,DO⊥BE,从而AO⊥平面BCDE,设AB=1,以B为原点,以BC为x轴,BD为y轴,建立空间直角坐标系,利用向量法能求出异面直线AB与DE所成角为60°.(2)求出平面ACE的法向量和平面ABE的法向量,由此利用向量法能求出二面角B﹣AE﹣C的余弦值.
【考点精析】本题主要考查了异面直线及其所成的角的相关知识点,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1 . 求证: 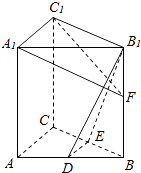
(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B分别在射线CM、CN(不含端点C)上运动,∠MCN= ![]() π,在△ABC中,角A、B、C所对的边分别是a、b、c.
π,在△ABC中,角A、B、C所对的边分别是a、b、c.
(Ⅰ)若a、b、c依次成等差数列,且公差为2.求c的值;
(Ⅱ)若c= ![]() ,∠ABC=θ,试用θ表示△ABC的周长,并求周长的最大值.
,∠ABC=θ,试用θ表示△ABC的周长,并求周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的是(填序号)
①命题“x1 , x2∈M,x1≠x2 , 有[f(x1)﹣f(x2)](x2﹣x1)>0”的否定是“x1 , x2M,x1≠x2 , 有[f(x1)﹣f(x2)](x2﹣x1)≤0”;
②若一个命题的逆命题为真命题,则它的否命题也一定为真命题;
③已知p:x2+2x﹣3>0, ![]() ,若命题(q)∧p为真命题,则x的取值范围是(﹣∞,﹣3)∪(1,2)∪[3,+∞);
,若命题(q)∧p为真命题,则x的取值范围是(﹣∞,﹣3)∪(1,2)∪[3,+∞);
④“x≠3”是“|x|≠3”成立的充分条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第12界全运会于2013年8月31日在辽宁沈阳顺利举行,组委会在沈阳某大学招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如图所示的茎叶图(单位: ![]() ),身高在175
),身高在175![]() 以上(包括175
以上(包括175![]() )定义为“高个子”,身高在175
)定义为“高个子”,身高在175![]() 以下(不包括175
以下(不包括175![]() )定义为“非高个子”.
)定义为“非高个子”.

(1)如果用分层抽样的方法从“高个子”和“非高个子”中共抽取5人,再从这5人中选2人,求至少有一人是“高个子”的概率?
(2)若从身高180![]() 以上(包括180
以上(包括180![]() )的志愿者中选出男、女各一人,求这两人身高相差5
)的志愿者中选出男、女各一人,求这两人身高相差5![]() 以上的概率.
以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,椭圆C的长轴长为4.
,椭圆C的长轴长为4.
(1)求椭圆C的方程;
(2)已知直线l:y=kx+ ![]() 与椭圆C交于A,B两点,是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
与椭圆C交于A,B两点,是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国上是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准![]() (吨),用水量不超过
(吨),用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照
的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照![]() ,
, ![]() ,…,
,…, ![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.

(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)已知该市有80万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使![]() 的居民每月的用水量不超过标准
的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由;
的值,并说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com