
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
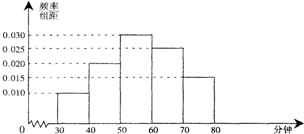 李克强总理4月22日(世界读书日前一天)在厦门大学考察时,指出世界读书日虽然只有一天,但我们应该天天读书,这种好习惯会让我们终身受益.
李克强总理4月22日(世界读书日前一天)在厦门大学考察时,指出世界读书日虽然只有一天,但我们应该天天读书,这种好习惯会让我们终身受益.| 非读书迷 | 读书迷 | 总计 | |
| 男 | 15 | ||
| 女 | 45 | ||
| 总计 |
| P(K2≥k1) | 0.100 | 0.050 | 0.010 | 0.001 |
| k1 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com