
【题目】函数![]()
![]() 部分图象如图所示.
部分图象如图所示.
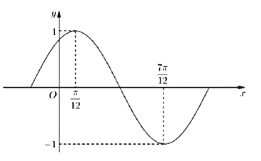
(1)求![]() 的最小正周期及解析式;
的最小正周期及解析式;
(2)设![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() .
.
【解析】
(1)由图可知A=1,![]() ,从而可求ω;再由图象经过点(
,从而可求ω;再由图象经过点(![]() ,1),可求得
,1),可求得![]() ;
;
(2)依题意g(x)化简整理为g(x)=![]() sin(2x
sin(2x![]() ),再利用正弦函数的性质结合x的范围求得g(x)的最大值和最小值.
),再利用正弦函数的性质结合x的范围求得g(x)的最大值和最小值.
(1)由图可知:![]() ,A=1,
,A=1,
∴T=π,
∴ω![]() 2,
2,
∴f(x)=cos(2x+![]() )
)
又∵图象经过点![]() ,
,
∴1=cos(2![]() ),
),
∴![]() 2kπ,k∈Z,
2kπ,k∈Z,
∴![]() 2kπ,k∈Z,
2kπ,k∈Z,
又∵|![]() |
|![]() ,
,
∴![]() ,
,
∴解析式为f(x)=cos(2x![]() );
);
(2)g(x)=f(x)+sin2x
=cos(2x![]() )+sin2x
)+sin2x
=cos2xcos![]() sin2xsin
sin2xsin![]()
![]() sin2x
sin2x![]() cos2x
cos2x
=![]() sin(2x
sin(2x![]() );当
);当![]() 时,2x
时,2x![]() ,
,
当2x![]() 时,即x=
时,即x=![]() 时,g(x)的最大值为
时,g(x)的最大值为![]() ,当2x
,当2x![]() ,即x=
,即x=![]() 时g(x)的最小值为
时g(x)的最小值为![]() ,
,
综上所述,![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】某家具厂有方木料90![]() ,五合板600
,五合板600![]() ,准备加工成书桌和书橱出售.已知生产第张书桌需要方木料O.l
,准备加工成书桌和书橱出售.已知生产第张书桌需要方木料O.l![]() ,五合板2
,五合板2![]() ,生产每个书橱而要方木料0.2
,生产每个书橱而要方木料0.2![]() ,五合板1
,五合板1![]() ,出售一张方桌可获利润80元,出售一个书橱可获利润120元.
,出售一张方桌可获利润80元,出售一个书橱可获利润120元.
(1)如果只安排生产书桌,可获利润多少?
(2)怎样安排生产可使所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】顺次连接椭圆![]() 的四个顶点恰好构成了一个边长为
的四个顶点恰好构成了一个边长为![]() 且面积为
且面积为![]() 的菱形。
的菱形。
(1)求椭圆![]() 的方程;
的方程;
(2)![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个不同点,若直线
上的两个不同点,若直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() (以
(以![]() 为坐标原点),线段
为坐标原点),线段![]() 上有一点
上有一点![]() 满足
满足![]() ,连接并延长交椭圆
,连接并延长交椭圆![]() 于点
于点![]() ,求椭圆
,求椭圆![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的方程为
的方程为![]() .
.
(1)当![]() 时,试确定曲线
时,试确定曲线![]() 的形状及其焦点坐标;
的形状及其焦点坐标;
(2)若直线![]() 交曲线
交曲线![]() 于点
于点![]() 、
、![]() ,线段
,线段![]() 中点的横坐标为
中点的横坐标为![]() ,试问此时曲线
,试问此时曲线![]() 上是否存在不同的两点
上是否存在不同的两点![]() 、
、![]() 关于直线
关于直线![]() 对称?
对称?
(3)当![]() 为大于1的常数时,设
为大于1的常数时,设![]() 是曲线
是曲线![]() 上的一点,过点
上的一点,过点![]() 作一条斜率为
作一条斜率为![]() 的直线
的直线![]() ,又设
,又设![]() 为原点到直线
为原点到直线![]() 的距离,
的距离,![]() 分别为点
分别为点![]() 与曲线
与曲线![]() 两焦点的距离,求证
两焦点的距离,求证![]() 是一个定值,并求出该定值.
是一个定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an} 满足a1=a,![]() =can+1﹣c(n∈N*),其中a、c为实数,且c≠0.
=can+1﹣c(n∈N*),其中a、c为实数,且c≠0.
(1)求数列{an} 的通项公式;
(2)设a=![]() ,c=
,c=![]() ,bn=n(1﹣an)(n∈N*),求数列 {bn}的前n项和Sn.
,bn=n(1﹣an)(n∈N*),求数列 {bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了![]() 三款软件,为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动,这三款软件的激活码分别为下面数学问题的三个答案:已知数列
三款软件,为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动,这三款软件的激活码分别为下面数学问题的三个答案:已知数列![]() ,其中第一项是
,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,再接下来的三项是
,再接下来的三项是![]() ,以此类推,试根据下列条件求出三款软件的激活码
,以此类推,试根据下列条件求出三款软件的激活码
(1)A款应用软件的激活码是该数列中第四个三位数的项数的平方
(2)B款应用软件的激活码是该数列中第一个四位数及其前所有项的和
(3)C款应用软件的激活码是满足如下条件的最小整数![]() :①
:①![]() ;②该数列的前
;②该数列的前![]() 项和为2的整数幂
项和为2的整数幂
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com